行星的热传导

约 5146 字大约 17 分钟...

零、引入

岩石圈弯曲研究表明，在地质时间尺度上，厚度为 25-50 公里的近地表区域表现出弹性行为。地震研究显示，地球地幔至 2885 公里深度均为固体，因能传播剪切波。为理解薄弹性壳的存在，需考虑固体岩石流变学随深度的变化。近地表岩石主要呈弹性行为，而深部岩石在地质时间尺度上必须表现出流体或蠕变行为以松弛应力。地幔岩石的流体行为还导致地幔对流及相关的地表板块运动。

实验室和理论研究表明，固体的流变学主要是温度的函数，因此，要理解地球的力学行为，必须了解其热结构。地幔岩石的流变学与温度随深度的函数直接相关，而这又取决于热量从内部散失到表面的速率。地球内热传递有传导、对流和辐射三种机制。传导通过分子碰撞传递热量；对流与介质运动相关；辐射在地球内部影响较小，其作用可并入热导率定义。在地球中，传导和对流均为重要的传热方式，如大陆地壳和岩石圈的温度分布主要受传导控制，而地幔深部的热传递以对流为主。

一、傅里叶热传导定律

热传导的基本关系，其在一维情况下的表达式为

q = - k \frac{d T}{d y}

表明热通量与温度梯度成正比，负号表示热流方向与温度升高方向相反。通过该定律，可计算通过材料的热通量，如通过平板材料时，热通量 $q = \frac{k Δ T}{l}$

1.1 热传导方程推导过程

在准备推导时，需要考虑流入和流出微元的热能平衡，如下图所示。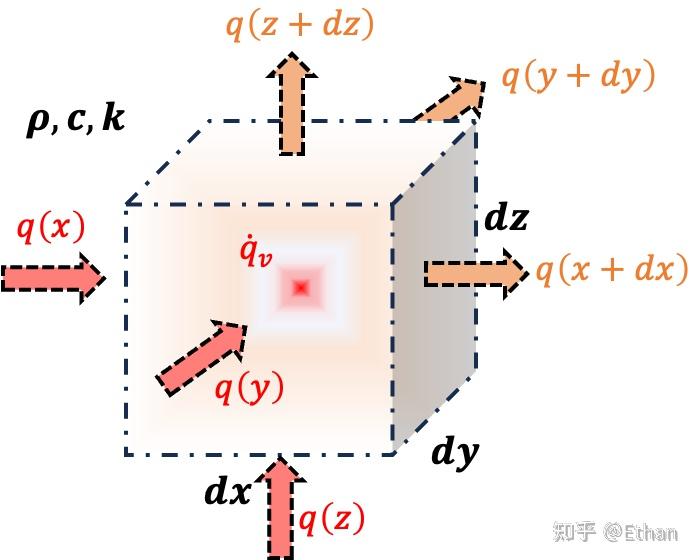

物体密度为 $ρ$ ,比热为 $c$ ,导热系数为 $k$ ,穿过每个表面的热通量为 $q_{x}$

此时，从能量平衡的关系来看，内能的变化是输入能量以及输出的能量的差值，另外，微元内产生的热量为因此，它们之间存在以下关系。

Δ U = E_{i n} - E_{o u t} + E_{s}

当时间内的温度变化为时，如下所示

Δ U = ρ c (d x d y d z) Δ T

进而考虑后如下式所示

E_{i n} = {q (x) d y d z + q (y) d x d z + q (z) d x d y} Δ t

E_{o u t} = {q (x + d x) d y d z + q (y + d y) d x d z + q (z + d z) d x d y} Δ t

最后的如下式所示

E_{s} = {\dot{q}}_{v} (d x d y d z) Δ t

将上述式代入公式(1)整理后得到式(2)

ρ c \frac{Δ T}{Δ t} = - \frac{q (x + d x) - q (x)}{d x} - \frac{q (y + d y) - q (y)}{d y} - \frac{q (z + d z) - q (z)}{d z} + {\dot{q}}_{v} (2)

现在，可以使用泰勒展开式近似如下

q (x + d x) ≒ q (x) + \frac{\partial q (x)}{\partial x} d x

q (x + d x) - q (x) ≒ \frac{\partial q (x)}{\partial x} d x

因此，应用傅里叶定律，上式变为

q (x + d x) - q (x) ≒ \frac{\partial q (x)}{\partial x} d x = k \frac{\partial^{2} T}{\partial x^{2}} d x

由上式可知(2)可如式变形

ρ c \frac{Δ T}{Δ t} = k \frac{\partial^{2} T}{\partial x^{2}} + k \frac{\partial^{2} T}{\partial y^{2}} + k \frac{\partial^{2} T}{\partial z^{2}} + {\dot{q}}_{v}

考虑到时间极限后如下式所示，

ρ c \frac{\partial T}{\partial t} = k \frac{\partial^{2} T}{\partial x^{2}} + k \frac{\partial^{2} T}{\partial y^{2}} + k \frac{\partial^{2} T}{\partial z^{2}} + {\dot{q}}_{v}

整理后得到下式

\frac{\partial T}{\partial t} = \frac{k}{ρ c} (\frac{\partial^{2} T}{\partial x^{2}} + \frac{\partial^{2} T}{\partial y^{2}} + \frac{\partial^{2} T}{\partial z^{2}}) + \frac{{\dot{q}}_{v}}{ρ c}

这样，就成功地推导出热传导方程了。

最后，使用拉普拉斯算子可以简单的表示热传导方程如下

\frac{\partial T}{\partial t} = \frac{k}{ρ c} \nabla^{2} T + \frac{{\dot{q}}_{v}}{ρ c}

1.2 运动介质的热传导方程

当介质本身以恒定速度 U 沿 x 方向运动（如侵蚀、沉积过程中的物质输运），热传导方程需考虑对流项（介质运动引起的热量输运）。设固定坐标系为 $(x, y)$ ，运动坐标系为 $(ξ, ζ)$ ，满足：

x = ξ + U t, y = ζ

其中 $ξ$ 和 $ζ$ 是随介质移动的坐标，U 为介质运动速度。

方程推导：从固定坐标系到运动坐标系

移动坐标系中的热传导方程 在运动坐标系中，热传导方程与静止介质相同（无对流项）： ${(\frac{\partial T}{\partial t})}_{ξ, ζ} = κ (\frac{\partial^{2} T}{\partial ξ^{2}} + \frac{\partial^{2} T}{\partial ζ^{2}})$
链式法则转换导数 固定坐标系中的时间导数需包含介质运动的影响： ${(\frac{\partial T}{\partial t})}_{x, y} = {(\frac{\partial T}{\partial t})}_{ξ, ζ} + \frac{\partial T}{\partial ξ} \cdot \frac{\partial ξ}{\partial t} = {(\frac{\partial T}{\partial t})}_{ξ, ζ} - U \frac{\partial T}{\partial ξ}$ 由于 $ξ = x - U t$ ，故 $\frac{\partial ξ}{\partial t} = - U$ 。
引入对流 - 传导方程 将运动坐标系中的方程代入固定坐标系，消去 ${(\frac{\partial T}{\partial t})}_{ξ, ζ}$ ，得到： $\frac{\partial T}{\partial t} + U \frac{\partial T}{\partial x} = κ (\frac{\partial^{2} T}{\partial x^{2}} + \frac{\partial^{2} T}{\partial y^{2}})$ 这即为对流 - 传导方程，左侧第二项 $U \frac{\partial T}{\partial x}$ 为对流项，描述介质运动引起的热量输运，右侧为扩散项。

(1) 侵蚀过程（以河流三角洲为例）

假设三角洲以恒定速度 $U_{0}$ 向海推进（图 4.60），沉积物高度 $h (x, t)$ 满足： $ξ = x - U_{0} t (随三角洲前沿移动的坐标)$ 方程简化为稳态形式（因形态不随 $ξ$ 变化）： $- U_{0} \frac{d h}{d ξ} = κ \frac{d^{2} h}{d ξ^{2}}$ 边界条件： $h (ξ = 0) = h_{0}$ （陆地边缘高度）， $h (ξ \to \infty) = 0$ （海底基线）。解得： $h = h_{0} \exp (- \frac{U_{0} ξ}{κ}) = h_{0} \exp [- \frac{U_{0}}{k} (x - U_{0} t)]$ 表明三角洲高度随距离指数衰减，斜率 ${(\frac{\partial h}{\partial x})}_{ξ = 0} = - \frac{U_{0} h_{0}}{κ}$ ，可通过实测地形反推输运系数 $κ$ （如密西西比河三角洲案例， $κ = 8.5 \times 10^{5} m^{2} / yr$ ）。

(2)沉积过程（冲积扇形成）

当沉积物以恒定通量 $S_{0}$ 从悬崖底部输入，方程为非稳态对流-传导问题，解为误差函数形式（类似热脉冲扩散）：

h = \frac{2 S_{0}}{k} [\sqrt{\frac{κ t}{π}} \exp (- \frac{x^{2}}{4 κ t}) - \frac{x}{2} erfc (\frac{x}{2 \sqrt{κ t}})]

悬崖处高度 $h_{0} \propto \sqrt{t}$ ，斜率与输运系数直接相关，适用于模拟冲积扇的时间演化。

对流 - 扩散耦合：首次将介质运动（如板块漂移、沉积物搬运）与热传导结合，适用于移动边界问题（如俯冲带热结构、侵蚀面迁移）。
Culling 模型类比：沉积物输运方程 $\frac{\partial h}{\partial t} = K \frac{\partial^{2} h}{\partial x^{2}}$ 与热传导方程形式一致（K 为输运系数），可借用热传导解（如误差函数、指数衰减）描述地形演化（如断层崖侵蚀、三角洲推进）。
实际应用：通过该方程，地质学家可量化侵蚀速率、沉积厚度与时间的关系，为盆地演化、海岸线变迁等提供理论支持。
对流项物理意义：介质运动导致热量（或沉积物）被 “平流” 输运，与扩散项（分子 / 颗粒随机运动）共同决定温度（或地形）分布。
相似解方法：通过坐标变换（如 $ξ = x - U t$ ）将非稳态问题转化为稳态，简化求解过程，适用于边界匀速移动的地质场景（如洋脊扩张、河流三角洲推进）。

二、行星表面热流

2.1 大陆热流值测量

早期通过洞穴和矿井温度测量估算近地表热梯度，准确测量则需在大陆地区钻深孔，深度超 300m 以避开气候影响。测量热梯度需使用热敏电阻，同时要防止钻井液循环干扰测量结果，热导率可在实验室通过特定装置测定。

2.2 海洋热流之测量

在海洋底部，利用携带热敏电阻的针状探针穿透沉积物测量近表面热流，海水温度相对稳定，热流受海水热液对流影响。沉积物热导率可通过热流探针中的加热器测定。

2.3 热流值测量结果

大陆平均热流为 $65 \pm 1.6 m W / m^{2}$ ，海洋平均热流为 $101 \pm 2.2 m W / m^{2}$ ，全球总表面热流为 $4.43 \times 10^{13} W$ ，平均表面热流为 $87 m W / m^{2}$ 。

三、行星内部热源

3.1 重力吸积产热

3.2 放射性元素生热

地球内部热量主要源于铀、钍和钾等放射性元素的衰变。根据地壳和地幔中放射性元素的浓度，可计算其生热率。例如，地幔中放射性元素的生热率约为 $7.38 \times 10^{- 12} W / k g$ 。

3.3 生热率变化

放射性元素的生热率随时间变化，30 亿年前的生热率约为现在的两倍。不同岩石类型中放射性元素浓度差异较大，如花岗岩中浓度较高，而 “亏损” 橄榄岩中浓度较低。

四、热传导方程及其应用

4.1 一维稳态热传导

在一维稳态且有体积生热的情况下，热传导方程为

0 = k \frac{d^{2} T}{d y^{2}} + ρ H

通过积分并结合边界条件，可求解温度分布，如在半空间模型中，得到温度表达式

T = T_{0} + \frac{q_{0}}{k} y - \frac{ρ H}{2 k} y^{2}

4.2 径向热传导

在球体或球壳中，推导得到热平衡方程

\frac{d q_{r}}{d r} + \frac{2 q_{r}}{r} = ρ H

进而得到温度分布方程

0 = k (\frac{d^{2} T}{d r^{2}} + \frac{2}{r} \frac{d T}{d r}) + ρ H

对其积分可得温度的一般表达式，在特定边界条件下可确定具体温度分布。

4.3 二维和三维热传导

推广到二维热传导时，能量守恒方程为

\frac{\partial q_{x}}{\partial x} + \frac{\partial q_{y}}{\partial y} = ρ H

结合傅里叶定律得到温度分布方程。无内部热源时，满足拉普拉斯方程。三维热传导方程可类似推广。

4.4 一维非稳态热传导方程

当介质中无内热源（ $H = 0$ ）时，热传导过程仅由温度随时间变化和空间扩散共同控制。考虑厚度为 $δ y$ 的微元体（图 4.5）：

净热流进出：流入热流 $q (y)$ ，流出热流 $q (y + δ y)$ ，净热流为： $q (y) - q (y + δ y) = - \frac{\partial q}{\partial y} δ y (傅里叶定律： q = - k \frac{\partial T}{\partial y})$
内能变化：微元体温度变化 $\frac{\partial T}{\partial t}$ 导致内能变化，单位体积热容为 $ρ c$ ，总内能变化： $ρ c \frac{\partial T}{\partial t} δ y \cdot 1 (单位面积)$
能量守恒：净热流等于内能变化，代入傅里叶定律： $ρ c \frac{\partial T}{\partial t} = k \frac{\partial^{2} T}{\partial y^{2}}$ 定义热扩散率 $κ = \frac{k}{ρ c}$ （单位： $m^{2} / s$ ），方程简化为： $\frac{\partial T}{\partial t} = κ \frac{\partial^{2} T}{\partial y^{2}} （一维非稳态热传导方程）$

核心物理量：热扩散率 $κ$ 与特征时间 $τ$

热扩散率 $κ$ :表征热量在介质中扩散的能力，结合热导率 k（传导能力）、密度 $ρ$ 和比热 c（储热能力）。 $κ ↑ 意味着热量扩散快（如金属）； κ ↓ 扩散慢（如岩石）$ ; 花岗岩、玄武岩等常见岩石典型值： $κ \approx 1 {mm}^{2} / s = 10^{- 6} m^{2} / s$
特征时间 $τ = \frac{l^{2}}{κ}$ **
物理意义：温度变化扩散至距离 l 所需的特征时间，体现扩散过程的时间 - 空间尺度关联。
地质实例：
- 地表昼夜温度变化穿透深度 $l \approx 0.17 m$ ， $τ \approx 1 天$ （ $κ = 1 {mm}^{2} / s$ ）。
- 地球整体冷却时间估算：若 $l \approx 6400 km$ ， $τ \approx 4 \times 10^{17} s \approx 10^{10} 年$ （远超实际年龄，因未考虑放射性热源和对流）。

4.5 瞬时加热或冷却（半无限空间）

考虑一个半无限半空间（ $y \geq 0$ ），初始时刻（ $t = 0$ ）温度均匀为 $T_{1}$ 。 $t > 0$ 时，表面（ $y = 0$ ）温度骤变为 $T_{0}$ 并保持恒定（加热： $T_{0} > T_{1}$ ；冷却： $T_{0} < T_{1}$ ）,目标是求解温度分布 $T (y, t)$ 和表面热流 $q (t)$ 。这一场景类似于岩浆侵入（围岩冷却）、海洋岩石圈冷却（海水降温）、地表温度骤变（如冰川消融）等情况。

此处运用的数学模型正是前面的一维非稳态热传导方程（无产热， $H = 0$ ）：

\frac{\partial T}{\partial t} = κ \frac{\partial^{2} T}{\partial y^{2}} $ $ 有 着 以 下 的 边 界 条 件 ： - $ T (0, t) = T_{0} (t > 0), $ - $ T (y, 0) = T_{1} (y > 0), $ - $ T (\infty, t) = T_{1} (t > 0) $ * * 引 入 无 量 纲 温 度 * * 定 义 归 一 化 温 度 $ θ = \frac{T - T_{1}}{T_{0} - T_{1}} $ ， 将 方 程 和 边 界 条 件 简 化 为 ： $ \frac{\partial θ}{\partial t} = κ \frac{\partial^{2} θ}{\partial y^{2}}, θ (0, t) = 1, θ (\infty, t) = 0, θ (y, 0) = 0 $ * * 相 似 变 量 法 （ 相 似 解 ） * * 观 察 到 问 题 无 特 征 长 度 ， 仅 由 热 扩 散 率 $ κ $ 和 时 间 t 控 制 ， 引 入 * * 相 似 变 量 * * ： $ $ η = \frac{y}{2 \sqrt{κ t}} (无量纲，融合空间与时间尺度)

假设 $θ$ 仅为 $η$ 的函数，即 $θ (y, t) = Θ (η)$ ，利用链式法则：

\frac{\partial θ}{\partial t} = \frac{d Θ}{d η} \cdot \frac{\partial η}{\partial t} = \frac{d Θ}{d η} \cdot (- \frac{η}{2 t})

\frac{\partial^{2} θ}{\partial y^{2}} = \frac{1}{4 κ t} \cdot \frac{d^{2} Θ}{d η^{2}}

代入原方程，消去 t 后得到常微分方程：

\frac{d^{2} Θ}{d η^{2}} + 2 η \frac{d Θ}{d η} = 0

求解常微分方程 令 $ϕ = \frac{d Θ}{d η}$ ，方程化简为：

\frac{d ϕ}{d η} = - 2 η ϕ ⟹ ϕ = C_{1} e^{- η^{2}}

对 $ϕ$ 积分得到 $θ$ 的表达式：

θ = c_{1} \int_{0}^{η} e^{- η^{' 2}} d η^{'} + c_{2}

其中 $η^{'}$ 是积分 dummy 变量（避免与上限 $η$ 混淆）。

应用边界条件 $Θ (0) = 1$ 、 $Θ (\infty) = 0$ ，得： $1 = c_{1} \int_{0}^{0} e^{- η^{' 2}} d η^{'} + c_{2} ⟹ c_{2} = 1$ $0 = c_{1} \cdot \frac{\sqrt{π}}{2} + 1 ⟹ c_{1} = - \frac{2}{\sqrt{π}}$

引入误差函数和余误差函数

Θ (η) = erfc (η) = 1 - erf (η)

其中，误差函数 $erf (η) = \frac{2}{\sqrt{π}} \int_{0}^{η} e^{- η^{' 2}} d η^{'}$ ，互补误差函数 $erfc (η) = 1 - erf (η)$ 。

温度解 还原为原始变量： $\frac{T - T_{1}}{T_{0} - T_{1}} = erfc (\frac{y}{2 \sqrt{κ t}})$

表面（ $y = 0$ ）： $erfc (0) = 1$ ，故 $T = T_{0}$ ，满足边界条件。
无穷深处（ $y \to \infty$ ）： $erfc (\infty) = 0$ ，故 $T = T_{1}$ ，符合初始条件。
时空演化：温度扰动随 t 扩散，特征深度为 $y \sim 2 \sqrt{κ t}$ （图 4.21）。温度解为互补误差函数形式： $\frac{T - T_{1}}{T_{0} - T_{1}} = erfc (\frac{y}{2 \sqrt{κ t}})$

热通量表达式

q = - k \cdot \frac{\partial}{\partial y} {[T_{1} + (T_{0} - T_{1}) \cdot erfc (\frac{y}{2 \sqrt{κ t}})]}_{y = 0}

由于 $T_{1}$ 是常数，导数为 0，简化为：

q = - k (T_{0} - T_{1}) \cdot \frac{\partial}{\partial y} erfc {(\frac{y}{2 \sqrt{κ t}})}_{y = 0} = - k (T_{0} - T_{1}) \cdot (- \frac{1}{\sqrt{π κ t}}) = k (T_{0} - T_{1}) \cdot \frac{1}{\sqrt{π κ t}}

热边界层厚度 定义边界层厚度为 $θ = 0.1$ 处的 y，查表得 $erfc (η_{T}) = 0.1 ⟹ η_{T} \approx 1.16$ ，故：

y_{T} = 2 η_{T} \sqrt{κ t} \approx 2.32 \sqrt{κ t}

表示温度显著变化的深度随时间平方根增长。

热通量表达式 记为 $T = T_{1} + (T_{0} - T_{1}) \cdot erfc (\frac{y}{2 \sqrt{κ t}})$ ，应用傅里叶定律 $q = - k {(\frac{\partial T}{\partial y})}_{y = 0}$ ，求导得：

\frac{\partial T}{\partial y} = (T_{0} - T_{1}) \cdot \frac{\partial}{\partial y} erfc (\frac{y}{2 \sqrt{κ t}}) = - \frac{T_{0} - T_{1}}{\sqrt{π κ t}} e^{- η^{2}} |_{η = 0} = - \frac{T_{0} - T_{1}}{\sqrt{π κ t}}

所以表面热流：

q = \frac{k (T_{0} - T_{1})}{\sqrt{π κ t}}

热流随时间递减， $t = 0$ 时理论上无穷大（因瞬时温度突变），实际中随时间趋于稳定。

4.6 温度周期性变化（半无限空间）

考虑一个半无限半空间（ $y \geq 0$ ， $y = 0$ 为地表，向下为正），地表温度随时间周期性变化： $T_{s} = T_{0} + Δ T \cos (ω t)$ ，其中， $T_{0}$ 为平均温度， $Δ T$ 为温度振幅， $ω = 2 π f$ 为角频率，f 为频率，周期 $τ = 1 / f = 2 π / ω$ （如昼夜周期 $τ = 1$ 天，季节周期 $τ = 1$ 年）。假设地表无内部热源（ $H = 0$ ），热传导为一维非稳态过程。这一场景可以应用于研究地球表面周期性温度变化（如昼夜、季节、冰川周期）如何影响地下温度分布。

这里还是考虑一维非稳态热传导方程（无产热， $H = 0$ ）：

\frac{\partial T}{\partial t} = κ \frac{\partial^{2} T}{\partial y^{2}}

有着以下边界条件：

$y = 0$ 处： $T (0, t) = T_{0} + Δ T \cos (ω t)$
$y \to \infty$ 处： $T \to T_{0}$ （深层温度不变）
初始条件： $t = 0$ 时，温度分布为 $T (y, 0) = T_{0}$ （可通过叠加原理简化）。

假设解的形式为

T (y, t) = T_{0} + Re [Θ (y) e^{i ω t}]

其中 $Θ (y)$ 为复振幅， $Re$ 表示实部。

代入热传导方程得：

i ω Θ = κ \frac{d^{2} Θ}{d y^{2}} $ $ 特 征 方 程 解 为 ： $ $ Θ (y) = C e^{- λ y} e^{- i λ y}, λ = \sqrt{\frac{ω}{2 κ}} $ $ 利 用 边 界 条 件 $ y \to \infty $ 时 $ Θ \to 0 $ ， 舍 去 增 长 项 ， 得 ： $ $ Θ (y) = A e^{- (1 + i) λ y} $ $ 由 $ y = 0 $ 处 $ T = T_{0} + Δ T \cos (ω t) $ ， 得 复 振 幅 $ A = Δ T $ ， 最 终 解 为 ： $ $ T (y, t) = T_{0} + Δ T e^{- λ y} \cos (ω t - λ y) $ $ 其 中 ， $ λ = \sqrt{\frac{ω}{2 κ}} $ $ 定 义 为 * * 衰 减 常 数 * * 。 * * 温 度 振 幅 衰 减 * * 地 下 温 度 波 动 振 幅 随 深 度 指 数 衰 减 ： $ $ 振幅 = Δ T \cdot e^{- λ y} = Δ T \cdot e^{- y / d_{ω}}

其中，皮肤深度（Skin Depth） $d_{ω}$ 为振幅衰减至表面值 $1 / e$ 时的深度：

d_{ω} = \sqrt{\frac{2 κ}{ω}} = \sqrt{\frac{κ τ}{π}}

实例：

昼夜变化（ $τ = 1$ 天， $κ = 1 {mm}^{2} / s$ ）： $d_{ω} = \sqrt{\frac{1 \times 10^{- 6} \times 86400}{π}} \approx 0.17 m$
季节变化（ $τ = 1$ 年， $κ = 1 {mm}^{2} / s$ ）： $d_{ω} = \sqrt{\frac{1 \times 10^{- 6} \times 3.15 \times 10^{7}}{π}} \approx 3.16 m$ 相位滞后 地下温度峰值滞后于地表温度峰值，相位差 $ϕ = λ y = y \sqrt{\frac{ω}{2 κ}}$ （弧度）。
当 $y = d_{ω}$ 时，相位差 $ϕ = 1$ 弧度（约 57.3°），即滞后约 $τ / (2 π)$ 时间。

钻孔温度测量校正 地表周期性温度波动会干扰深部热流测量，需通过皮肤深度确定钻孔深度。例如，若需避免季节波动影响，钻孔深度应大于 $3 d_{ω}$ （此时振幅衰减至 <5%）。

冰川周期的温度印记 冰川期地表温度下降，间冰期回升，形成长周期（ $τ \sim 10^{4} - 10^{5}$ 年）波动。通过皮肤深度公式：

d_{ω} = \sqrt{\frac{κ τ}{π}} \sim \sqrt{\frac{1 \times 10^{- 6} \times 10^{4} \times 3.15 \times 10^{7}}{π}} \sim 100 m

此类波动可在数百米深度的岩心中保留温度变化记录，用于反推古气候。

热扩散率反演 通过测量不同深度的温度振幅和相位差，可反推热扩散率 $κ$ 。例如，已知某深度 $y_{1}$ 和 $y_{2}$ 处的振幅比，可计算 $κ$ ：

\frac{Δ T (y_{1})}{Δ T (y_{2})} = e^{- (y_{1} - y_{2}) / d_{ω}} ⟹ κ = \frac{ω (y_{1} - y_{2})^{2}}{2 \ln (Δ T (y_{1}) / Δ T (y_{2}))}

物理量	表达式	说明
温度分布	$T = T_{0} + Δ T e^{- λ y} \cos (ω t - λ y)$	含衰减和相位滞后的周期性解
皮肤深度	$d_{ω} = \sqrt{\frac{2 κ}{ω}} = \sqrt{\frac{κ τ}{π}}$	振幅衰减至 $1 / e$ 的深度
相位差	$ϕ = λ y = y \sqrt{\frac{ω}{2 κ}}$	深度 y 处的滞后相位
通过求解周期性边界条件下的热传导方程，揭示了地表温度波动向地下传播的规律：振幅随深度指数衰减，相位随深度滞后。皮肤深度是衡量波动穿透能力的关键参数，其与周期平方根成正比，决定了不同时间尺度的温度变化影响深度。这一理论在地质热流测量、古气候重建和热物性反演中具有重要应用，为理解地球浅层热过程提供了数学基础。