随机事件与概率
1.1 随机试验和随机事件
- 随机现象: 自然界中的客观现象,当人们观测它时,所得结果不能预先确定,而仅仅是多种可能结果之一。
- 随机试验: 随机现象的实现和对它某个特征的观测。
- 基本事件: 随机试验中的每个单一结果,犹如分子中的原子,在化学反应中不可再分。
e.g. 硬币抛3次,有8种结果:正正正、正正反、正反正……这8种可能结果每一个都是基本事件。 - 随机事件: 简称事件,在随机试验中我们所关心的可能出现的各种结果,它由一个或若干个基本事件组成。通常用英文大写字母表示或{一种叙述}来表示。
- 样本空间: 随机试验中所有基本事件所构成的集合,通常用
- **必然事件(
- **不可能事件(
1.2 事件的运算
- 子事件
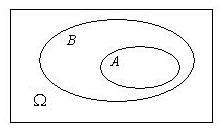
- 事件的和(
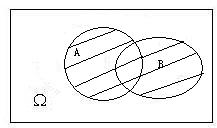
- 事件的积(
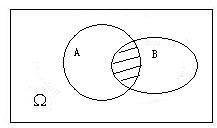
- 对立事件
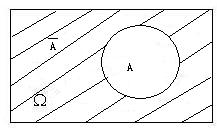
- **事件
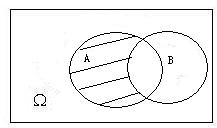
- De Morgan対偶法则及其推广
上式可推广到n个事件:
1.3 概率的定义
概率是随机事件发生可能性大小的数字表征,其值在0和1之间,即概率是事件的函数。概率有以下定义:
1.3.1 古典概率
设一个试验有N个等可能的结果,而事件
古典概型有两个条件:
- 有限性,试验结果只有有限个(记为n),
- 等可能性,每个基本时间发生的可能性相同。
**注:**古典概率可引申出“几何概率”。
1.3.2 概率的统计定义
古典概率的两个条件往往不能满足,但可以将事件的随机试验独立反复做n次(Bernouli试验),设事件
**注:**不能写为
,因为 不是n的函数。
1.3.3 主观概率
主观概率可以理解为一种心态或倾向性。究其根由,大抵有二:一是根据其经验和知识,二是根据其利害关系。该学派在金融和管理有大量的应用,这一学派成为Bayes学派。
1.3.4 概率的公理化定义
对概率运算规定一些简单的基本法则:
- 设
- 设
- 若事件
注:
- 一般情况下,
,
1.4 古典概率计算
1.4.1 排列组合
- **选排列:**从n个不同元素中取r个不同取法(
- **重复排列:**从n个不同元素中可重复地取r个不同取法(
- **组合:**同选排列,但不考虑次序,
注:
- 排列英文为Permutation,组合英文为Combination.
为1。当r不是非负整数时,记号 没有意义. - 一些书中将组合写成
或 ,更通用的是 .
1.4.2 其他公式
- 组合系数
- n个相异物件分成k堆,各堆物件数分为
1.5 条件概率、乘法公式、独立性
条件概率就是知道了一定信息下得到的随机事件的概率。设事件
为事件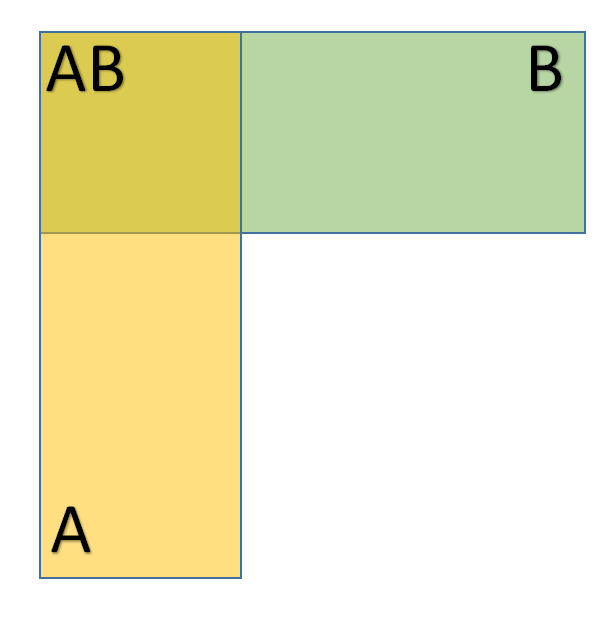
**注:**事实上,我们所考虑的概率都是在一定条件下计算的,因为随机试验就是在一定条件下进行的。
1.5.1 条件概率性质
给定
- 若
1.5.2 乘法公式
由
注: 右边看似麻烦,其实容易算,左边看似简单,但是难算。
1.5.3 独立性
如果
定义:
1.6 全概公式
设
设
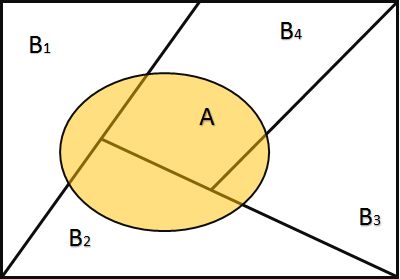 推导:
推导:
**注:**有时不易直接计算事件
的概率,但是在每个 上 的条件概率容易求出
全概公式可以应用于赌徒输光问题、敏感问题的调查等
1.7 逆概公式(Bayes公式)
设
**注:**当有因果关系互换时必须用Bayes公式。
贝叶斯公式在生活中的应用很多,例如疾病检测避免假阳性等
1.8 事件的独立性
设
设
上面有
**注:**独立(independent)和不相容(exclusive)是不同的两个概念,前者有公共部分,后者没有公共部分,独立一定相容。
1.9独立试验序列概型
定理(独立试验序列概型计算公式) 设单次试验中,事件A发生的概率为
证: 在n次重复试验中,记B,B,,…,B为构成事件“A发生k次”的那些试验结果,于是有:
- (1)“A发生k次”=
- (2)
- (3)
注意,“n次重复试验”中的“重复”二字,是指这n次试验中各次试验的条件组是相同的.因此,这不仅意味着在各次试验中A发生的概率都是力(于是A发生的概率也都是q),而且还有各次试验的结果间是互相独立的含义.定理证明过程中的(2),就是基于这两个含义而得出的.在具体应用时也要注意这“重复”二字,