随机变量(Random variable): 值随机会而定的变量,研究随机试验的一串事件。可按维数分为一维、二维至多维随机变量。按性质可分为离散型随机变量以及连续型随机变量。
**分布(Distribution):**事件之间的联系,用来计算概率。
示性函数(Indication function):
,事件有随机变量表示出来,称为事件的示性函数。
1.离散型随机变量: 设为一随机变量,如果只取有限个或可数个值,则称为一个(一维)离散型随机变量。 2.概率函数: 设为一随机变量,其全部可能值为,则称为的概率函数。 3.概率分布: 离散型随机变量的概率分布可以用分布表来表示:
| 可能值 | | | ... | | ... |
|---|
| 概率 | | | ... | | ... |
4.概率分布函数:
定义:设为一随机变量,则函数
称为的分布函数。(注:这里并未限定为离散型的,它对任何随机变量都有定义。)
性质:时,有. 当时,;当时,.
离散型随机变量分布函数:
对于离散型随机变量,。
定义:设某事件在一次试验中发生的概率为,先把试验独立地重复n次,以记在这n次试验中发生的次数,则取值,且有
称服从二项分布,记为.
服从二项分布的条件:1. 各次试验的条件是稳定的,即事件的概率在各次试验中保持不变;2. 各次试验的独立性
定义:设随机变量的概率分布为
则称服从参数为的Poisson分布,并记.
特点::
- 描述稀有事件发生概率
- 作为二项分布的近似。若,其中很大,很小,而不太大时(一般),则的分布接近泊松分布.
推导: 若事件,且很大,很小,而不太大时,设,
1.连续型随机变量: 设为一随机变量,如果不仅有无限个而且有不可数个值,则称为一个连续型随机变量。
2.概率密度函数: 定义:
- 设连续型随机变量有概率分布函数,则的导数称为的概率密度函数。
性质:
- 对于所有的,有;;
- 对于任意的,有.
注: 对于任意的,有. 假设有总共一个单位的质量连续地分布在上,那么表示在点的质量密度且表示在区间上的全部质量。
3.概率分布函数:设为一连续型随机变量,则
定义:如果一个随机变量具有概率密度函数
其中,则称为正态随机变量,并记为.特别地,的正态分布成为标准正态分布。用和表示标准正态分布的分布函数和密度函数。
性质: 正态分布的密度函数是以为对称轴的对称函数,称为位置参数,密度函数在处达到最大值,在和内严格单调。的大小决定了密度函数的陡峭程度,通常称为正态分布的形状参数。 若,则.
图像(密度和分布函数图):
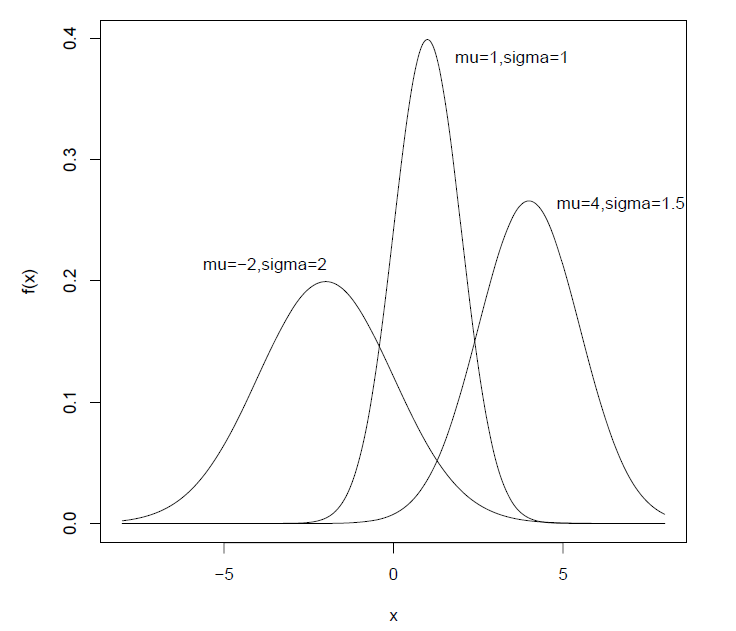
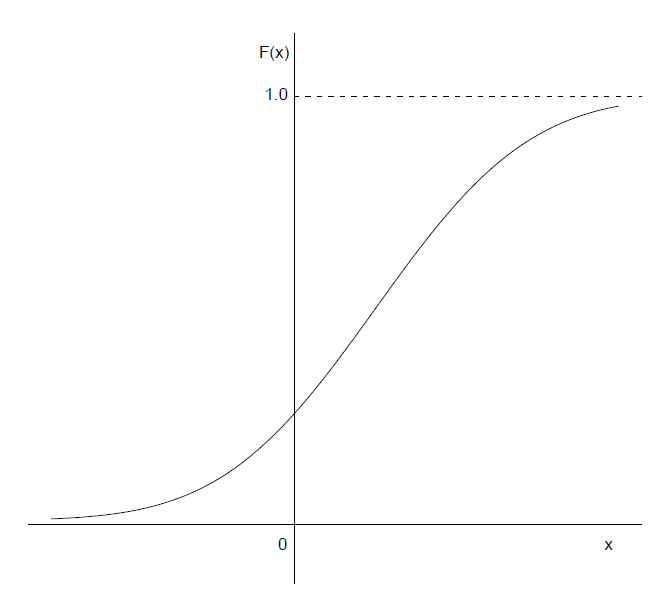
定义 : 若随机变量具有概率密度函数
其中为常数,则称服从参数为的指数分布。
概率分布函数:
性质:
无后效性,即无老化,要来描述寿命(如元件等)的分布。
证明: “无老化”就是说在时刻正常工作的条件下,其失效率总保持为某个常数,与无关,可表示
为失效率,失效率越高,平均寿命就越小。
图像(密度函数):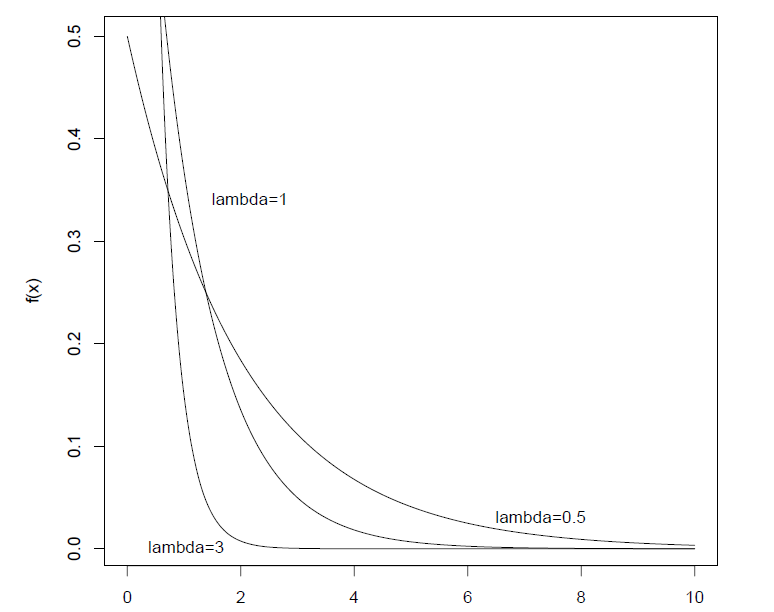
定义:设,如果分布具有密度函数
则该分布为区间上的均匀分布。
概率分布函数:
性质:
设.如果每个都是一个随机变量,,则称为维随机变量或者随机向量。
如果每一个都是一个离散型随机变量,,则称为一维离散型随机变量。设的所有可能取值为,则称
为维随机变量的概率函数,这也是其联合分布。其具有下列性质
注: 对于高维离散型随机变量,一般不使用分布函数
定义: 设是某一试验之下的完备事件群,分别以记事件的概率,则.将试验独立地重复次,以记在这次试验中事件出现的次数,则为一个维随机向量。该分布记作.
概率分布函数:
为维连续型随机变量,如果存在上的非负函数,使得对任意的 ,有
则称为的概率密度函数,也称 为 的联合分布密度 (简称联合密度).有
则称为为的(联合)分布函数。其中分布函数具有下述性质:
- 单调非降;
- 对任意的,有;
连续型随机向量属于更一般的平面子集D的概率为
集合的要求涉及到勒贝格积分,这里不做讨论。一般的开集、并 集及其有限运算都符合条件。
- 联合密度不是概率,其在平面点(x,y)的小邻域的积分才是概率;
- 类似于物理学中质量面密度的概念;
- p(x, y) 是一个全平面上有定义的二元非负函数。实际中使用的二元 密度一般在全平面连续,或者除去个别几条线之后是连续的。
- (1.6) 中的集合 D 可以是全平面,所以 ∞ −∞ ∞ −∞ p(x, y)dxdy = 1
- 概率的计算转化为二重积分,P((X,Y)∈D) 的概率是以D为底面、 以密度函数曲面为顶面的曲顶柱体的体积。
因为的每个分量都是一维随机变量,故它们都有各自的分布,这些都是一维分布,称为随机向量或其分布的边缘分布。
离散型随机向量 行和与列和就是边缘分布。即固定某个,即可计算边缘分布,故有
行和与列和就是边缘分布。即固定某个,即可计算边缘分布,故有
连续型随机向量
为求某分量的概率密度函数,只需把中的固定,然后对在到之间做定积分,如
注: 二维正态分布的边缘分布密度分别是一维正态分布和。因此联合分布可推边缘分布,而边缘分布不可推联合分布
称随机变量相互独立,
离散型随机变量
则联合分布律等于各自的边缘分布律的乘积,即
其中为的值域中的任意一点。
连续型随机变量
则联合密度等于各自的边缘密度的乘积,即
更具一般地
设为个随机变量,如果它们的联合分布函数等于各自边缘分布函数的乘积,即
则称随机变量相互独立。
一些重要的结论
## 2.6 随机变量的条件分布
设为二维离散型随机变量,对于给定的事件,其概率,则称
为在给定的条件下的条件分布律。类似的,称
为在给定的条件下的条件分布律。
设为二维连续型随机变量,对于给定条件下的条件概率密度为
类似的,在下的条件概率密度为
二维正态分布时,其联合密度分布等于条件密度分布的乘积。
最简单的情形,是由一维随机变量的概率分布去求其一给定函数的分布。较为常见的,是由的分布去求的分布。更一般地,由的分布去求的分布,其中.
1.离散型分布的情形: 设的分布律为
,令,则的分布律为
即把可以取的不同值找出来,把与某个值相应的全部值的概率加起来,即得取这个值的概率。
2.连续型分布的情形
一个变量的情况
设有密度函数.设,是一个严格单调的函数,即当时,必有或当时,必有.又设的导数存在。由于的严格单调性,其反函数存在,且的导数也存在。有的密度函数为
严格单调是一个苛刻的条件,许多常见的函数无法满足,此时只好直接去求所要的分布函数,不要考虑反函数。
多个变量的情形
以两个为例,设的密度函数,都是的函数:
要求的概率密度函数.假定到的一一对应变换有逆变换:
即雅可比行列式
不为0.在的平面上任取一个区域,变换后到平面的区域,则有
随机变量和的密度函数
设的联合密度函数为,的密度函数:
一般的,. 若独立,则.
两个独立的正态变量的和仍服从正态分布,且有关的参数相加,其逆命题也成立。
随机变量商的密度函数 设的联合密度函数为,的密度函数:
一般的,. 若独立,则.
引入两个重要的特殊函数:
和
其中,
卡方分布,记作
密度函数
性质:1. 设独立,,则
2. 若独立,且都服从指数分布,则
分布,记作
设,独立,,而,则.
密度函数:
性质:密度函数关于原点对称,其图形与正态分布的密度函数的图形相似。
分布,记作
设独立,,而,则
密度函数:
三大分布的几个重要性质
设独立同分布,有公共的正态分布.记.则.
设的假定同1,则
设独立,各有分布,各有分布,则
若,则



 行和与列和就是边缘分布。即固定某个
行和与列和就是边缘分布。即固定某个