板块的应变与弯曲

约 4647 字大约 15 分钟...

地壳板块的挠曲

薄而有弹性的地表板块构成了岩石圈，它漂浮在下方相对呈流体状态的地幔之上。这些板块承受着各种载荷，例如火山、海山等，在它们的重压下，岩石圈会发生弯曲。通过将观测到的岩石圈挠曲或弯曲情况与已知的地表载荷联系起来，我们可以推断出板块的弹性属性和厚度。

我们首先建立板块在受力和力矩作用下的弯曲理论。该理论可以通过将褶皱模拟为受水平压力作用的弹性板块变形，来帮助我们理解山脉带中的褶皱系列。此外，还可以运用该理论模拟火成岩侵入体上方地层的上拱现象（3.12）。

0.重点公式一览

\begin{aligned} 力矩平衡 d M = V \cdot d x + P \cdot d w \overset{对 x 求 两 次 导}{\to} \frac{d^{2} M}{d x^{2}} = - q + P \frac{d^{2} w}{d x^{2}} \\ 挠曲刚度 M = - \frac{E h^{3}}{12 (1 - ν^{2})} \frac{d^{2} w}{d x^{2}} = - D \frac{d^{2} w}{d x^{2}} \\ 四阶挠曲方程 D \frac{d^{4} w}{d x^{4}} + P \frac{d^{2} w}{d x^{2}} = q (x) \\ 挠曲参数(flexture parameter) α = {(\frac{4 D}{Δ ρ g})}^{1 / 4} \\ 最大弯曲应力(bendiing stress) σ_{max} = \frac{E h}{2 (1 - ν^{2}) R} = \frac{6 M}{h^{2}} \end{aligned}

薄板模型： $厚度 h ≪ 长度 L$ ，仅在 x-y 平面弯曲（圆柱弯曲，沿 z 方向无限长）。 小挠度假设：挠度 $w (x) ≪ L$ ，忽略几何非线性，曲率近似为 $1 / R \approx - d^{2} w / d x^{2}$ 。 平面应力状态：板表面无垂直应力（ $σ_{y y} = 0$ ），且沿厚度方向（y 方向）的应变 $ε_{z z} = 0$ （因板无限长，z 方向无变形）。

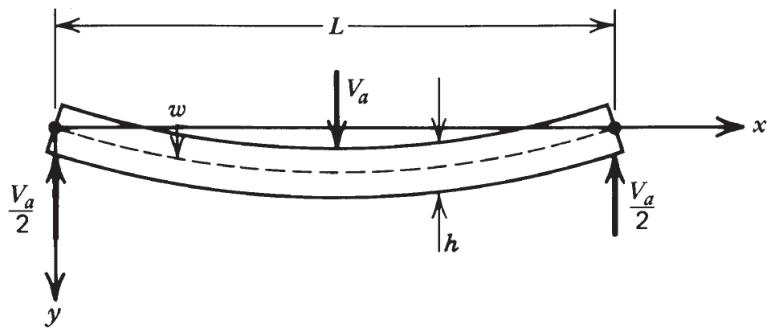
2. 力与力矩平衡

考虑微元 dx 的受力（图 3.10）：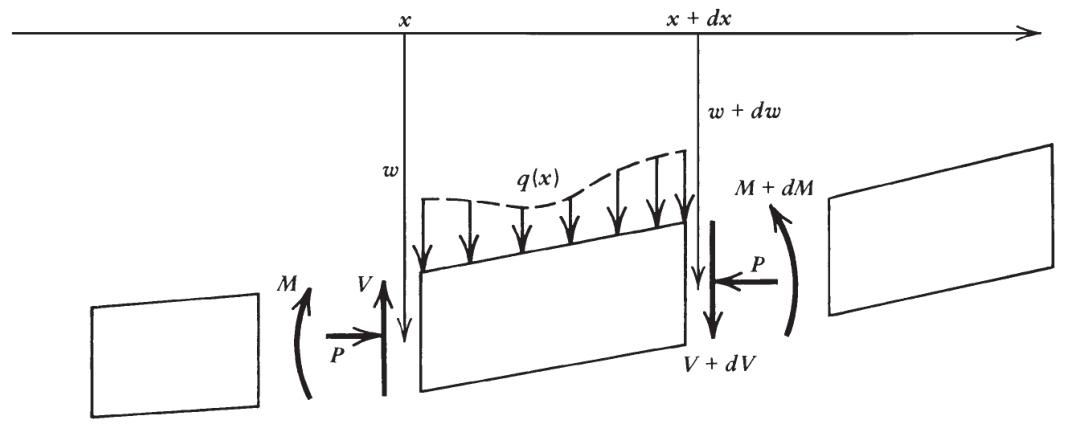

1.在 x 和 x + dx 之间，沿 z 方向每单位长度的向下载荷为 q (x) dx
2.沿 z 方向每单位长度的净剪力 V 作用在垂直于图面的板横截面上(所有剪应力积分的合力)
3.沿 z 方向每单位长度的水平力 P 作用在板上(假设 P 与 x 无关)
4.沿 z 方向每单位长度作用在板横截面上的净弯矩 M(正应力 σxx在截面上的积分)

垂直力平衡：载荷 $q (x)$ 与剪切力 $V$ 平衡

d V = - q \cdot d x \to \frac{d V}{d x} = - q （3.57）

力矩平衡：弯曲力矩 M、剪切力 V 和水平力 P 的力矩平衡

d M = V \cdot d x + P \cdot d w \to \frac{d M}{d x} = V + P \frac{d w}{d x} ​ （3.59）

力矩 $M$ 和 $M + d M$ 共同作用，在微元上产生净逆时针扭矩dM。
力 $V$ 和 $V + d V$ 相隔距离dx（一个无穷小力臂），并以顺时针方向在微元上施加净扭矩Vdx。（在计算剪切力引起的力矩时，从 $x$ 到 $x + d x$ 的 $V$ 的变化可忽略不计。）
水平力 P 通过其相关力臂 $- d w$ 在微元上施加净逆时针扭矩 $- P d w$ 。（注意，从 x 到 $x + d x$ 时，dw为负值。）

我们可以对公式（3.59）关于x求导，并代入公式（3.57），来消去剪切力V。由此得到：

\frac{d^{2} M}{d x^{2}} = - q + P \frac{d^{2} w}{d x^{2}} . (3.60)

3. 弯曲力矩与曲率的关系

弯曲应力分布：板弯曲时，上表面压缩（ $σ_{x x} > 0$ ），下表面拉伸（ $σ_{x x} < 0$ ），中性面（ $y = 0$ ）无应变。

几何关系：距中性面 y 处的应变

ε_{x x} = - \frac{Δ l}{l} = \frac{y}{R} = - y \frac{d^{2} w}{d x^{2}}

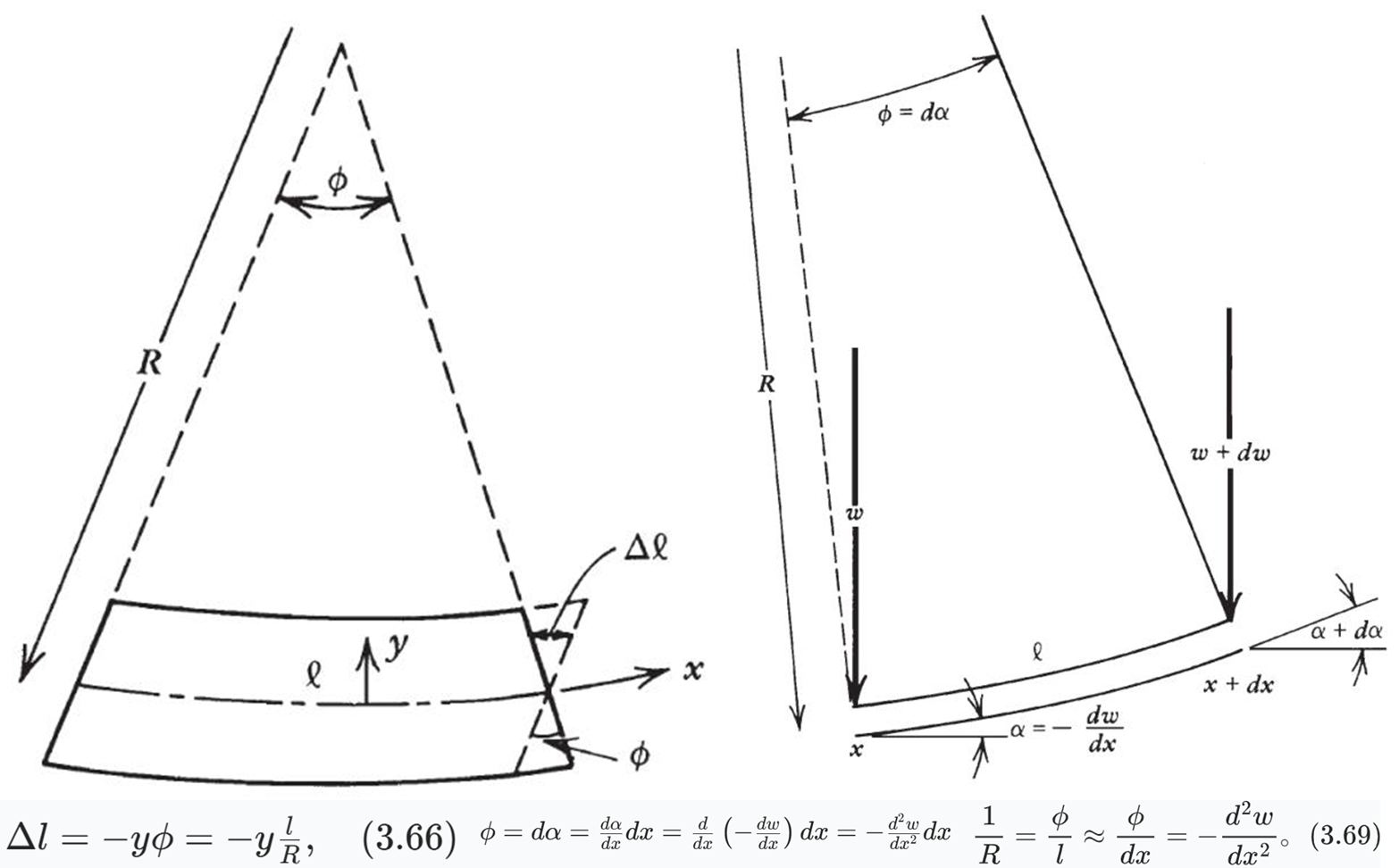
小角度 $ϕ$ （以弧度为单位）等于 $1 / R$ 。

平面应力下，胡克定律简化为 $σ_{x x} = \frac{E}{1 - ν^{2}} ε_{x x}$ （因 $σ_{z z} = 0$ ， $ε_{z z} = - \frac{ν}{E} σ_{x x}$ ）。

力矩积分：弯曲力矩 M 为纤维应力对中性面的力矩积分： $M = \int_{- h / 2}^{h / 2} σ_{x x} y d y = \frac{E}{1 - ν^{2}} \int_{- h / 2}^{h / 2} ε_{x x} y d y = - \frac{E h^{3}}{12 (1 - ν^{2})} \frac{d^{2} w}{d x^{2}}$
挠曲刚度(flexture ) $D = \frac{E h^{3}}{12 (1 - ν^{2})}$ ，则： $M = - D \frac{d^{2} w}{d x^{2}} （3.73）$
弯曲应力的最大值出现在板的上下表面（ $y = \pm h / 2$ ），代入 $σ_{x x} = \frac{E}{1 - ν^{2}} ε_{x x}$ 和 $ε_{x x} = \pm \frac{h}{2 R}$ （R 为曲率半径， $1 / R = - d^{2} w / d x^{2}$ ），可得：$$\sigma_{\text{max}} = \frac{E h}{2(1-\nu^2) R} = \frac{6M}{h^2}$$

4. 四阶挠曲方程

将 $M = - D \frac{d^{2} w}{d x^{2}}$ 代入力矩平衡方程（3.59）：

\frac{d}{d x} (- D \frac{d^{2} w}{d x^{2}}) = V + P \frac{d w}{d x} ⟹ - D \frac{d^{3} w}{d x^{3}} = V + P \frac{d w}{d x}

再对 x 求导，并利用垂直力平衡方程（3.57， $d V / d x = - q$ ）

- D \frac{d^{4} w}{d x^{4}} = \frac{d V}{d x} + P \frac{d^{2} w}{d x^{2}} ⟹ D \frac{d^{4} w}{d x^{4}} = q - P \frac{d^{2} w}{d x^{2}}

最终得到四阶挠曲微分方程（核心方程 2）： $D \frac{d^{4} w}{d x^{4}} + P \frac{d^{2} w}{d x^{2}} = q (x) （3.74）$

方程物理意义

载荷项 $q (x)$ ：包括表面载荷（如火山质量）和静水恢复力（如海水或地壳填充下弯空间产生的向上力，见 3.13 节）。
水平力项 P：若存在水平压缩 / 拉伸力（如构造应力），影响弯曲形态（屈曲分析见 3.11 节）。
挠曲刚度 D：反映板的抗弯曲能力，与板厚 h 的三次方成正比（厚度增加，刚度急剧增大）。

5.实际应用

5.1 岩石圈板块的弯曲

将弹性板挠曲理论应用于地球岩石圈，考虑载荷作用下岩石圈的挠曲变形时，引入静水压力恢复力（hydrostatic restoring force），分析海洋和大陆岩石圈在不同载荷下的平衡方程。

岩石圈作为弹性板漂浮在 “流体” 地幔上，受表面载荷（如火山、沉积物）作用时发生挠曲，需考虑载荷下方地幔被低密度物质（水 / 地壳）替换产生的浮力效应。有以下基本假设：

岩石圈为薄弹性板，厚度为h，密度为 $ρ_{m}$ （地幔密度）。
载荷引起的挠曲挠度w较小，适用线性弹性理论。
垂直柱内物质守恒，低密度物质（海水 / 地壳）填充挠曲产生的空隙。

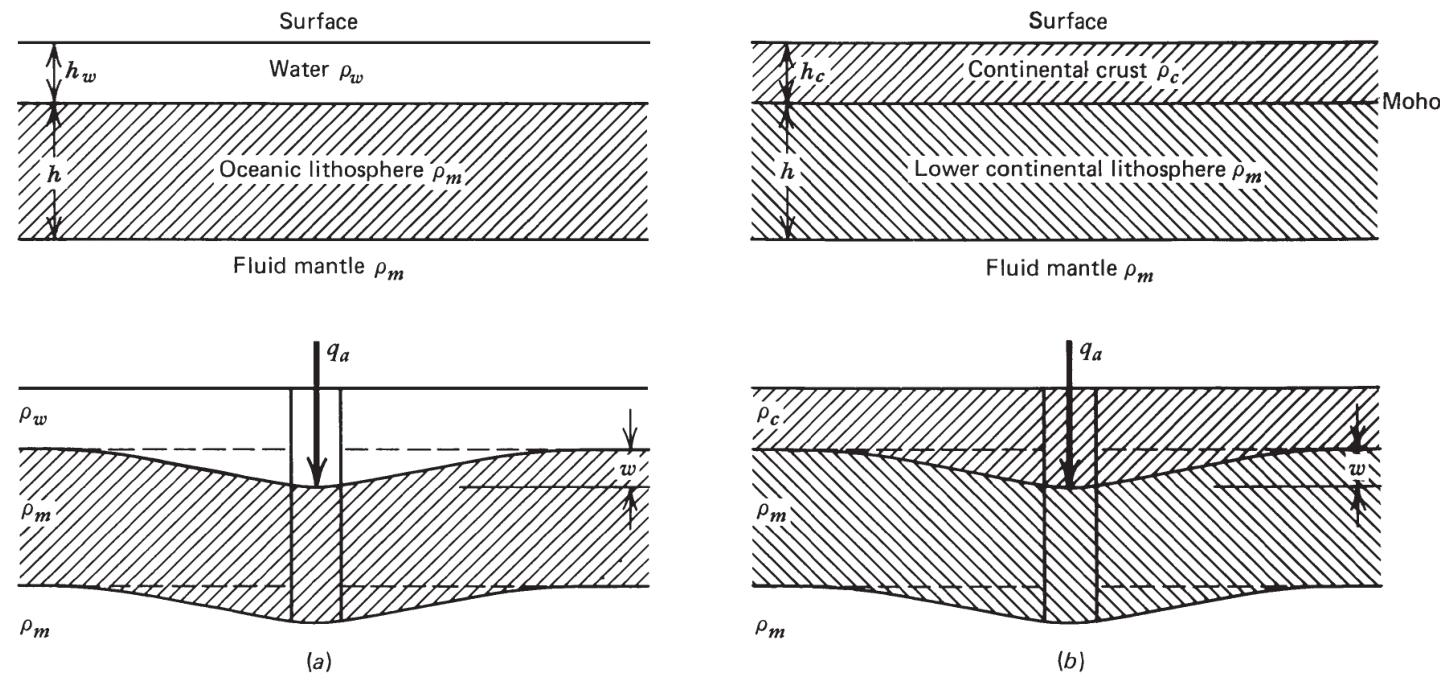
海洋岩石圈的挠曲（图a）

初始状态：海水厚度 $h_{w}$ ，密度 $ρ_{w}$ ；岩石圈厚度h，密度 $ρ_{m}$ ，漂浮于地幔（密度同 $ρ_{m}$ ）。 挠曲后：岩石圈下弯w，海水填充空隙，形成新的垂直柱：

柱底压力（未挠曲区）： $ρ_{w} g h_{w} + ρ_{m} g (h + w)$
柱底压力（挠曲区）： $ρ_{w} g (h_{w} + w) + ρ_{m} g h$
静水恢复力（向上）：两者压力差为 $(ρ_{m} - ρ_{w}) g w$ ，由地幔与海水的密度差产生。 表面载荷为 $q_{a} (x)$ ，净载荷 $q = q_{a} - (ρ_{m} - ρ_{w}) g w$ （恢复力抵消部分载荷）。代入挠曲方程（3.74），得：

D \frac{d^{4} w}{d x^{4}} + (ρ_{m} - ρ_{w}) g w = q_{a} (x) （3.103）

其中 $D = \frac{E h^{3}}{12 (1 - ν^{2})}$ 为挠曲刚度。

大陆岩石圈的挠曲（图b）

初始状态：大陆地壳厚度 $h_{c}$ ，密度 $ρ_{c}$ ；岩石圈（含地壳）漂浮于地幔（密度 $ρ_{m}$ ）。 挠曲后：岩石圈下弯w，地壳岩石填充空隙，Moho 面下弯w，形成新的垂直柱：

柱底压力（未挠曲区）： $ρ_{c} g h_{c} + ρ_{m} g (h + w)$
柱底压力（挠曲区）： $ρ_{c} g (h_{c} + w) + ρ_{m} g h$
静水恢复力（向上）：压力差为 $(ρ_{m} - ρ_{c}) g w$ ，由地幔与地壳的密度差产生。 表面载荷为 $q_{a} (x)$ ，净载荷 $q = q_{a} - (ρ_{m} - ρ_{c}) g w$ 。代入挠曲方程得：

D \frac{d^{4} w}{d x^{4}} + (ρ_{m} - ρ_{c}) g w = q_{a} (x) （3.106）

与海洋情况形式相同，但密度差为 $(ρ_{m} - ρ_{c})$ 。

5.2 岛链载荷

火山岛弧链作为载荷会引起岩石圈挠曲，我们可以使用四阶微分方程来描述这个现象，来

以夏威夷岛链为例，研究火山岛链作为线载荷引起的岩石圈挠曲变形。火山岛链（如夏威夷）由一系列火山和海山组成，形成线性载荷，导致下方岩石圈弯曲，表现为中央凹陷（如夏威夷深海）和外围前隆（forebulge）。模型具有以下简化假设：

线载荷假设：岛链载荷简化为沿直线分布的集中力 $V_{0}$ （单位长度载荷，N/m），作用于 $x = 0$ 处（图 3.29）。
对称性：载荷对称，仅需分析 $x \geq 0$ 区域，且 $x \to \infty$ 时挠度 $w \to 0$ 。
静水恢复力：海洋环境中，密度差 $Δ ρ = ρ_{m} - ρ_{w}$ 产生向上恢复力（ $ρ_{m}$ 为地幔密度， $ρ_{w}$ 为海水密度）。

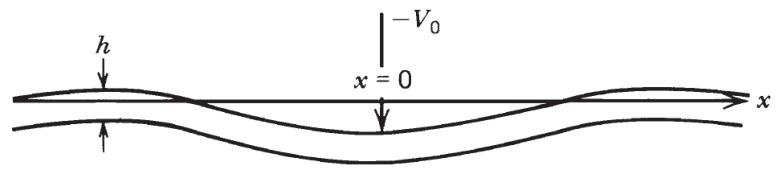
平衡方程：忽略水平力（ $P = 0$ ），挠曲方程为（3.125）：

D \frac{d^{4} w}{d x^{4}} + Δ ρ g w = 0, Δ ρ = ρ_{m} - ρ_{w}

5.2.1 微分方程求解

通解形式：方程为四阶常系数线性齐次微分方程，特征根为复数，通解为指数衰减振荡函数：

w = e^{x / α} (c_{1} \cos \frac{x}{α} + c_{2} \sin \frac{x}{α}) + e^{- x / α} (c_{3} \cos \frac{x}{α} + c_{4} \sin \frac{x}{α}) 3.126

其中，挠曲参数(flexture parameter) $α = {(\frac{4 D}{Δ ρ g})}^{1 / 4}$ （3.127），表征挠曲影响范围。

怎么算出来的通解你先别管，因为我实在不会

通过边界条件可以解出四个常数c1、c2、c3、c4：

对称性： $d w / d x = 0$ 于 $x = 0$ （载荷中心斜率为零）。
远场条件： $x \to \infty$ 时 $w \to 0$ ，故 $c_{1} = c_{2} = 0$ 。
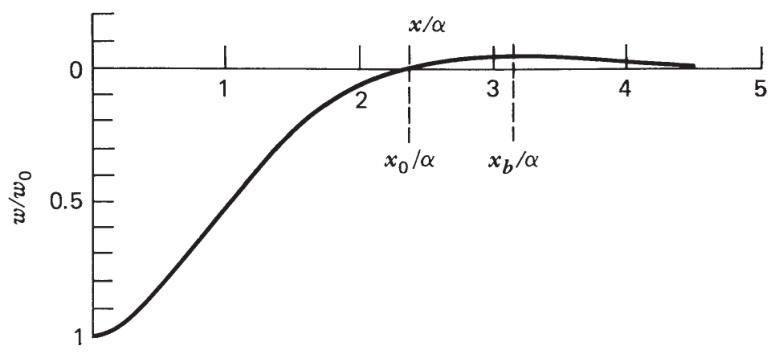
载荷平衡：通过剪切力积分确定 $c_{3} = c_{4}$ ，最终特解为： $w = w_{0} e^{- x / α} (\cos \frac{x}{α} + \sin \frac{x}{α}), w_{0} = \frac{V_{0} α^{3}}{8 D}$

5.2.2 方程分析

挠曲参数 $α$ 的意义：

控制挠曲影响范围，与挠曲刚度 D 和密度差 $Δ ρ$ 相关：$$\alpha \propto D^{1/4}, \quad D = \frac{E h^3}{12(1-\nu2)}$$
通过前隆位置 $x_{b} = π α$ 可直接估算 $α$ （如夏威夷 $x_{b} \approx 250$ km，得 $α = 80$ km）。

中央凹陷：中央凹陷由岛链载荷直接导致，在 $x = 0$ 处挠度最大（ $w_{0}$ ），随距离指数衰减。

前隆（Forebulge）：在 $x_{b} = π α$ 处出现微小上翘（ $w_{b} \approx - 0.0432 w_{0}$ ），是岩石圈弯曲的标志性特征。

岩石圈强度影响：

断裂模型中前隆幅度更大（ $w_{b} = - 0.0670 w_{0}$ vs. 完整模型的 $w_{b} = - 0.0432 w_{0}$ ），说明岩石圈完整性显著影响挠曲形态，断裂降低刚度，增大挠度。

5.2.3 地质意义

厚度估算实例：

完整岩石圈模型：代入 $α = 80$ km， $Δ ρ = 2300$ kg/m³， $g = 10$ m/s²，得 $D = 2.4 \times 10^{23}$ N・m，进一步算出 $h = 34$ km（取 $E = 70$ GPa， $ν = 0.25$ ）。
断裂岩石圈模型：若岛链处岩石圈断裂（如火山活动弱化岩石圈），边界条件变为 $x = 0$ 处无弯矩（ $d^{2} w / d x^{2} = 0$ ），解得挠度加倍（ $w_{0} = V_{0} α^{3} / (4 D)$ ），估算 $h = 49$ km（图 3.31-3.32）。

地质意义

通过岛链挠曲分析，可推断不同区域岩石圈厚度（如海洋岩石圈约 30-50 km），为板块构造、地震带划分提供依据。
问题 3.19-3.20 涉及最大弯曲应力计算，结合 $M = - D d^{2} w / d x^{2}$ ，可评估岩石圈内部应力状态（如夏威夷最大应力约 900 MPa）。

5.3 洋壳俯冲

海洋岩石圈在俯冲带海沟处的弹性弯曲，建立末端载荷作用下的挠曲模型。海沟是大洋岩石圈俯冲至地幔的边界，俯冲前岩石圈受重力作用发生强烈弯曲，形成深海沟（如马里亚纳海沟）和外围前隆。模型有以下的简化：

末端载荷：岩石圈视为半无限长弹性板（ $x \geq 0$ ），末端（海沟轴， $x = 0$ ）受垂直载荷 $V_{0}$ （向下为正）和弯矩 $M_{0}$ （逆时针为正），模拟俯冲板块的重力拖拽。
远场条件： $x \to \infty$ 时挠度 $w \to 0$ ，忽略水平力（ $P = 0$ ）。
平衡方程：同海洋岩石圈挠曲方程（3.125），考虑静水恢复力（密度差 $Δ ρ = ρ_{m} - ρ_{w}$ ）： $D \frac{d^{4} w}{d x^{4}} + Δ ρ g w = 0$

5.3.1 微分方程求解

通解形式：四阶方程的通解为指数衰减振荡函数（同上面一节）：

w = e^{- x / α} (c_{3} \cos \frac{x}{α} + c_{4} \sin \frac{x}{α})

其中 $α = {(\frac{4 D}{Δ ρ g})}^{1 / 4}$ 为挠曲参数，控制弯曲衰减速度。

通过边界条件可以解出两个常数c3、c4：

末端弯矩： $x = 0$ 处弯矩 $M = - M_{0} = - D \frac{d^{2} w}{d x^{2}}$ 得 $c_{4} = - \frac{M_{0} α^{2}}{2 D} (3.149)$
末端剪力： $x = 0$ 处剪力 $V = - V_{0} = - D \frac{d^{3} w}{d x^{3}}$ ，得 $c_{3} = \frac{(V_{0} α + M_{0}) α^{2}}{2 D} (3.150)$ 。

代入常数后，挠度为（3.151）：

w = \frac{α^{2} e^{- x / α}}{2 D} [(V_{0} α + M_{0}) \cos \frac{x}{α} - M_{0} \sin \frac{x}{α}]

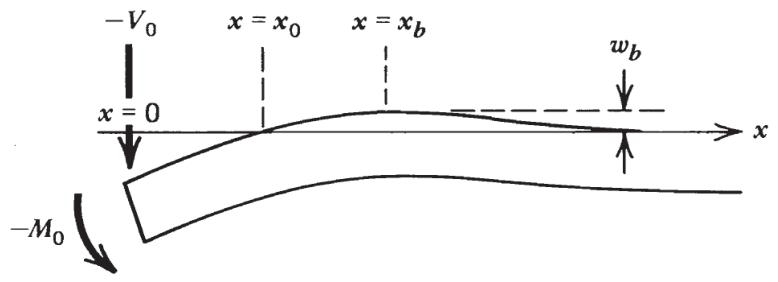
5.3.2 方程分析

前隆与凹陷分布：

中央凹陷：海沟轴（ $x = 0$ ）处挠度最大，随x增大指数衰减。
前隆位置：通过斜率为零（ $d w / d x = 0$ ）解得前隆中心位于 $x_{b} = x_{0} + \frac{π}{4} α$ ，前隆半宽 $x_{b} - x_{0} = \frac{π}{4} α$ （3.156），是岩石圈弹性厚度的直接标志。

通用挠曲剖面：

无量纲化处理后，得到通用曲线 $w / w_{b} \sim (x - x_{0}) / (x_{b} - x_{0})$ ，适用于所有末端载荷挠曲问题（图 3.34a）。

弯曲力矩与剪切力：

弯矩 $M (x)$ ：由 $M = - D \frac{d^{2} w}{d x^{2}}$ ，最大弯矩位于海沟轴外侧，导致岩石圈上部压缩、下部拉伸（图 3.34b）。
剪切力 $V (x)$ ：由 $d M / d x = V$ ，最大剪切力位于前隆附近（图 3.34c）。

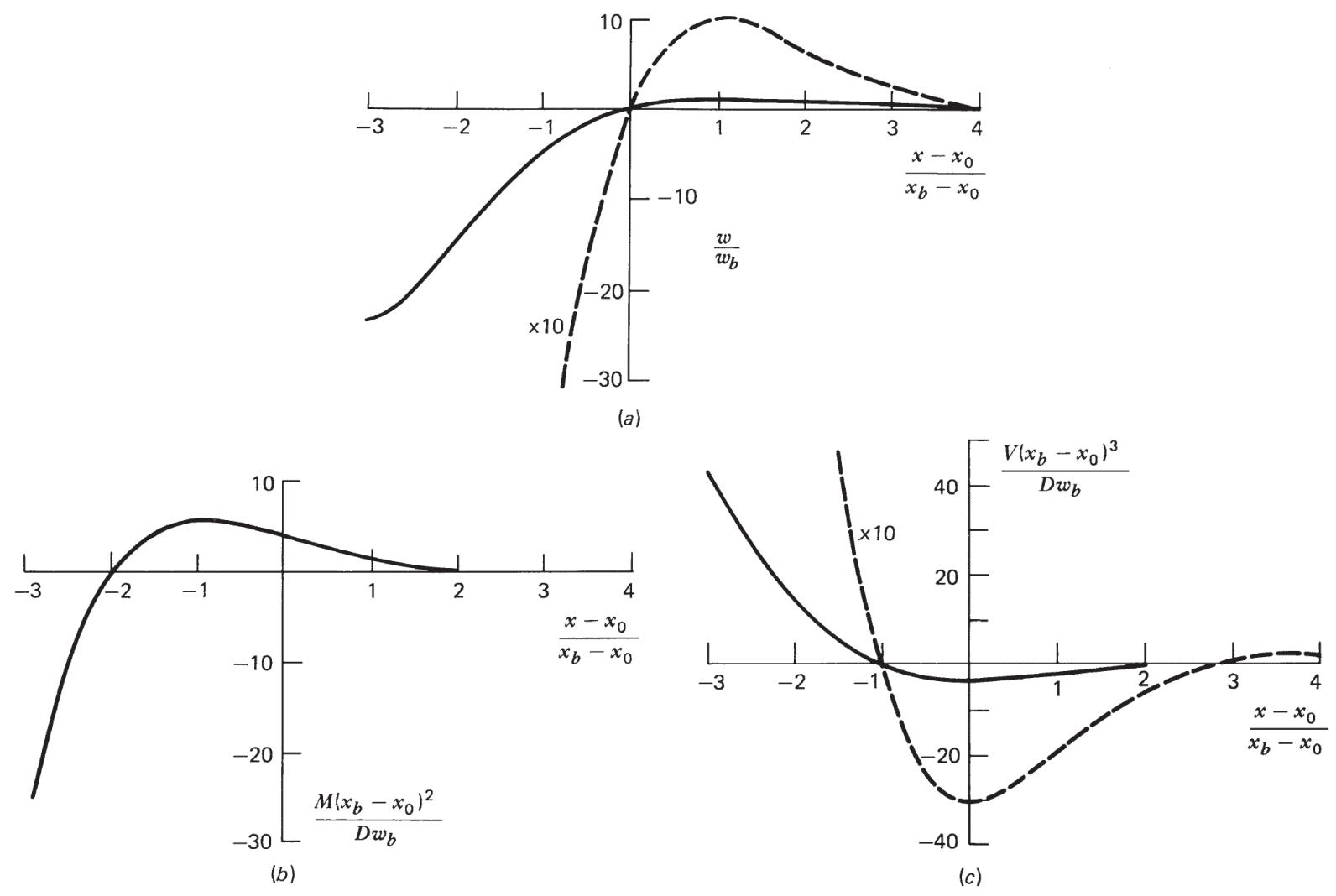
最大弯曲应力：

岩石圈底部拉伸应力最大，计算公式为： $σ_{max} = \frac{6 M}{h^{2}}$
马里亚纳海沟案例中，最大应力达 900 MPa，接近深部地幔的屈服强度，暗示岩石圈可能发生塑性变形（见第 7 章）。

5.3.3 地质意义

马里亚纳海沟实例：

数据拟合：取前隆半宽 $x_{b} - x_{0} = 55$ km，前隆高度 $w_{b} = 0.5$ km，计算得 $α = 70$ km，挠曲刚度 $D = 1.4 \times 10^{23}$ N・m，弹性厚度 $h = 28$ km（3.156）。
结果意义：与岛链载荷估算的岩石圈厚度（30-50 km）一致，验证弹性板模型的适用性。

部分海沟实测曲率远超理论预测，推测岩石圈在高应力下发生塑性屈服（非弹性变形），需结合塑性理论进一步分析（第 7 章内容）。

5.4 水平挤压

弹性板在水平压缩载荷下的屈曲（Buckling）现象，分析板从稳定平面状态转变为弯曲状态的临界条件，及其在地质构造（如褶皱带）中的应用。山脉带中的褶皱（Fold trains）被认为是地层在水平挤压下发生屈曲的结果，需通过弹性板理论分析临界载荷与褶皱波长。模型有以下的简化：

两端简支（Pinned）的弹性板，长度L，承受均匀水平压缩力P（单位长度力，N/m），忽略垂直载荷（ $q = 0$ ）。
假设小挠度、线性弹性，屈曲后板呈正弦曲线弯曲 $w (x)$ 。
平衡方程：结合挠曲方程（3.74）与水平力P，得：$$D \frac{d^4 w}{dx^4} + P \frac{d^2 w}{dx^2} = 0 \quad \text{（3.87）}$$ 其中 $D = \frac{E h^{3}}{12 (1 - ν^{2})}$ 为挠曲刚度， $w (x)$ 为垂直挠度。

5.4.1 微分方程求解

通解形式：进行两次积分可以得到一个二阶的微分方程

D \frac{d^{2} w}{d x^{2}} + P w = c_{1} x + c_{2} . (3.88)

通过边界条件可以解出两个常数c1、c2：

简支端——端点没有施加扭矩： w在 $x = 0$ 处为零，在 $x = L$ 处为零； $d^{2} w / d x^{2}$ 在 $x = 0$ 和 $x = L$ 处也为零可以解得 $c 1 = c 2 = 0$ , 则方程简化为

D \frac{d^{2} w}{d x^{2}} + P w = 0 . (3.89)

方程（3.89）是二阶常系数线性齐次微分方程，有通解

w = c_{1} s i n {(\frac{P}{D})}^{1 / 2} x + c_{2} c o s {(\frac{P}{D})}^{1 / 2} x, (3.90)

还是因为w在 $x = 0$ 处为零，在 $x = L$ 处为零—— $c 2 = 0$ , 但w在 $x = L$ 处也必须为零，这意味着若 $c_{1} \neq 0$ ，则

\sin [{(\frac{P}{D})}^{1 / 2} L] = 0 (3.92)

可以很容易的解出

P = \frac{n^{2} π^{2}}{L^{2}} D \overset{当 n = 1 时 ， P 取 最 小 值}{\to} P_{c} = \frac{π^{2}}{L^{2}} D

此时 $P_{c}$ 是板的最小屈曲载荷。若水平力 P 小于这个临界值（即特征值），板在施加的载荷下不会发生挠曲，即 $c_{1} = 0$ 或 $w = 0$ 。

5.4.2 方程分析

正弦通解的分析

屈曲波长：基频模式（ $n = 1$ ）的波长 $λ = 2 L$ ，即板长L对应半波长（图 3.22b）。
多模式屈曲： $n > 1$ 时出现多个褶皱，波长 $λ = \frac{2 L}{n}$ ，但临界载荷随 $n^{2}$ 增大，故基频模式最易发生（最小 $P_{c}$ ）。

临界应力计算：

临界载荷 $P_{c} = σ_{c} h$ ，其中 $σ_{c}$ 为临界应力，h为板厚： $σ_{c} = \frac{π^{2} D}{L h} = \frac{π^{2} E h^{2}}{12 (1 - ν^{2}) L}$
实例（完整岩石圈）：取 $h = 50$ km， $E = 100$ GPa， $ν = 0.25$ ， $L = 1000$ km，得 $σ_{c} = 6.4$ GPa，远超过构造应力（典型 10 MPa），故岩石圈不易屈曲。

薄弹性层屈曲计算：

若层厚 $h = 1$ km（如沉积岩），其他参数不变， $σ_{c} = 900$ MPa，接近岩石抗压强度，可能发生屈曲形成小型褶皱（如沉积层褶皱）。

振幅不可解：线性理论仅能确定临界载荷和屈曲波长，无法计算变形幅度（需非线性理论，考虑大变形几何非线性）。

5.4.3 地质意义

根据上面的临界应力计算和薄弹性层屈曲计算可知，岩石圈因厚度大、临界应力极高，在水平构造应力下更易发生断裂而非屈曲。薄弹性层（如地层夹层）临界应力低，是褶皱构造的主要成因（需考虑周围介质约束，如 3.12 节侵入体上拱）。

地层并非完全自由或简支，周围岩石的摩擦力、重力等需纳入模型,固定端或自由端需调整边界条件，但简支是最简化且典型的地质场景（如地层两端受限）。复杂场景需额外进行数值模拟。