陨石撞击坑和冲击动力学

约 4916 字大约 16 分钟...

一、利用撞击坑统计法对地质单元进行定年（统计法）

通过分析天体表面撞击坑的大小、数量及其分布规律，建立撞击坑参数与地质单元形成时间的定量关系，从而推断地质单元的年龄。该方法基于 “撞击坑累积效应”—— 较古老的地质单元因暴露时间更长，表面会累积更多撞击坑，尤其是大直径撞击坑的密度与年龄呈显著正相关。

1.1 撞击坑大小 - 频数关系早期研究

1.1.1 相对年龄判别依据

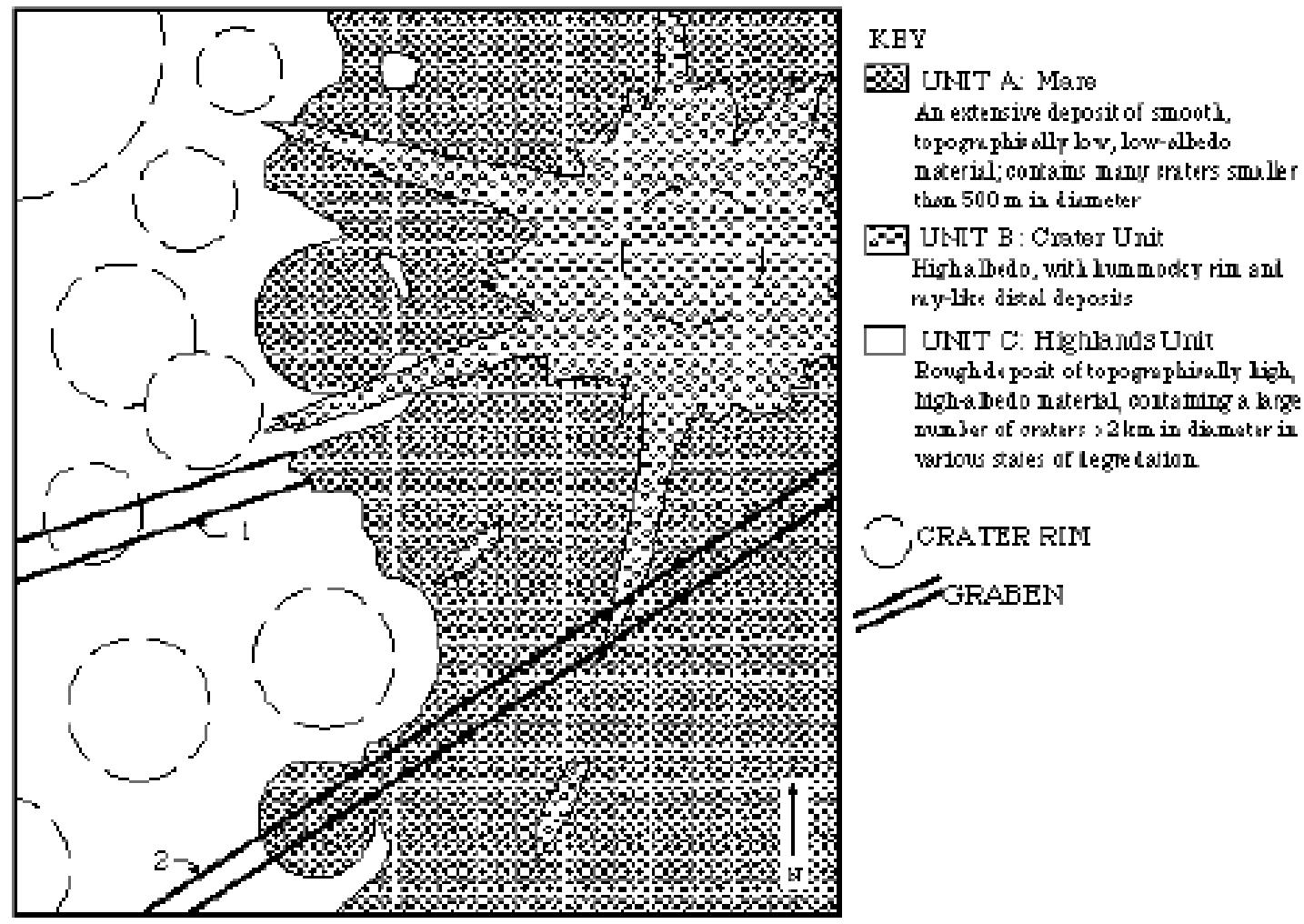
地质单元的相对年龄可通过三类关系判别：

叠置关系：若撞击坑的溅射席或熔岩流覆盖在某地质单元之上，则被覆盖的单元形成时间更早，因其先存在并被后期撞击产物覆盖。
交切关系：当皱脊、月溪等地质构造被撞击坑边缘或溅射物交切时，被交切的构造形成时间早于撞击事件，即相关地质单元年龄更老。
密度差异：在同等面积内，直径相近的撞击坑密度越高，地质单元年龄越大。这是因为老单元经历了更长时间的撞击累积，单位面积上的撞击坑数量随时间逐渐增加。

1.1.2 早期数学模型构建

Fauth（1907）的开创性发现：在《The Moon in Modern Astronomy》中首次提出撞击坑直径 D 与频率 N 呈双曲线关系，即 $N \propto 1 / D^{2}$ ，表明大撞击坑数量随直径增大呈平方反比减少。

Macdonald（1931）的对数坐标拟合：通过统计月球表面撞击坑数据，发现在对数坐标系中， $\log N$ 与 $\log D$ 呈线性关系，斜率约为 $- 1.9$ ，即 $\log N = - 1.9 \log D + 常数$ ，初步建立了撞击坑大小与频数的定量关联。

Cross（1966）的区域特征系数：提出公式 $N = 10^{10} \frac{C}{D^{2}}$ ，其中：

N 表示在 $10^{12} m^{2}$ 面积上直径大于 D（单位：m）的撞击坑数量（单位： $m^{- 2}$ ）；
C 是无量纲的区域特征系数，与地质单元年龄正相关 —— 老区域因撞击累积时间长，C 值更大（如云海、静海、阿尔芬斯区域的 C 分别为 1.4、1.0、2.5）。该公式的局限性在于 C 不仅受年龄影响，还与统计的直径 D 相关，且不同区域因观测分辨率差异（如有的区域只能提取 $D > 10 km$ 的坑，有的可提取 $D > 1 km$ 的坑），导致定年精度受限。

1.2 Neukum 撞击坑大小 - 频数关系及月球撞击坑累积分布年代模型

1.2.1 模型核心假设与分解公式

德国学者 Gerhard Neukum 提出撞击坑累积频数公式 $N (D, t) = G (D) \cdot F (t)$ ，将撞击坑数量分解为两部分：

$G (D)$ 为仅依赖直径 D 的普适函数，表示任意区域、任意时间下撞击坑大小与频数的内在规律（如大坑与小坑的数量比例）；
$F (t)$ 为仅依赖时间 t 的累积函数，表示自地质单元形成至 t 时刻，撞击坑数量随时间的增长效应。

\begin{aligned} N = D^{a_{1} + a_{2} l o g D + a_{3} (l o g D)^{2} + \dots a_{11} (l o g D)^{10}} \cdot 10^{a_{0}} = G (D) \cdot F (t) \\ G (D) = D^{a_{1} + a_{2} l o g D + a_{3} (l o g D)^{2} + \dots a_{11} (l o g D)^{10}} = D^{α (D)} \\ F (t) = N (1, t) = 5.44 \cdot 10^{- 14} (e^{6.93 t} - 1) + 8.38 \cdot 10^{- 4} t = 10^{a_{0}} \end{aligned}

1.2.2 多项式拟合与区域统计

通过统计月球 18 个典型区域（如澄海、雨海）的撞击坑数据，在对数坐标系中对 $G (D)$ 进行高次多项式拟合，得到：

\log N = a_{0} + a_{1} \log D + a_{2} (\log D)^{2} + \dots + a_{11} (\log D)^{11}

其中，系数 $a_{0} = - 3.0768$ （澄海区域基准值）， $a_{1} = - 3.6269$ ， $a_{2} = 0.4366$ 等，适用于 $10 m \leq D \leq 300 km$ 的直径范围。该公式本质上是对早期 $N \propto 1 / D^{2}$ 关系的修正，通过高阶项拟合复杂的大小 - 频数分布。

1.同期区域相似性：同一年龄的不同地质区域，相同直径的撞击坑频数相近。例如，年龄均为 $3.9 Ga$ 的 A 区域和 B 区域，直径 10 km 的撞击坑数量均约为 5 个 /km²，1 km 的坑均约为 600 个 /km²，反映撞击过程在空间上的随机性。 2.异期频数比例性：不同年龄区域的撞击坑频数比仅由时间决定，即 $\frac{N_{1} (D, t_{1})}{N_{2} (D, t_{2})} = \frac{F (t_{1})}{F (t_{2})}$ 。若 A 区域年龄为 $t_{1}$ ，B 区域为 $t_{2}$ ，且 A 的 10 km 坑数是 B 的 5 倍，则 A 的 1 km 坑数也约为 B 的 5 倍，体现大小坑频数随时间变化的一致性。

Neukum撞击坑大小-频数关系及月球撞击坑累积分布年代模型

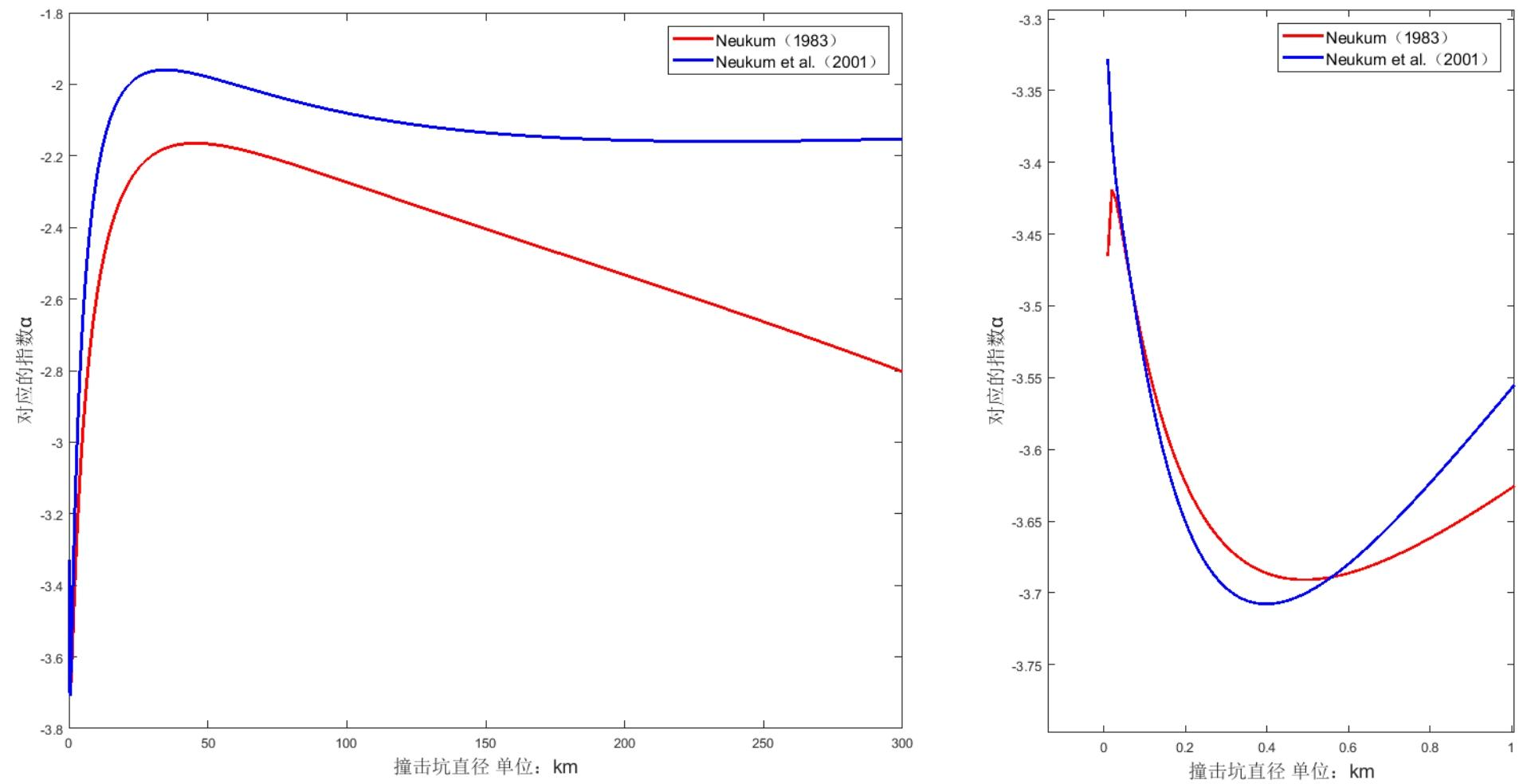
\begin{aligned} G (D) = D^{a_{1} + a_{2} l o g D + a_{3} (l o g D)^{2} + \dots a_{11} (l o g D)^{10}} = D^{α (D)} \\ α (D) = a_{1} + a_{2} l o g D + a_{3} (l o g D)^{2} + \dots a_{11} (l o g D)^{10} \\ N = D^{a_{1} + a_{2} l o g D + a_{3} (l o g D)^{2} + \dots a_{11} (l o g D)^{10}} \cdot 10^{a_{0}} \end{aligned}

1.2.4 绝对年龄标定与公式

利用 Apollo 和 Luna 任务返回的月岩样品（已知同位素年龄），将其对应区域的撞击坑频数 $N (D \geq 1 km)$ 与年龄 t 拟合，得到：

N (D \geq 1) = 5.44 \times 10^{- 14} (e^{6.93 t} - 1) + 8.38 \times 10^{- 4} t

式中 t 为地质单元年龄（单位：Ga）。例如，月球高地的 $N (D = 1) = (3.6 \pm 1.1) \times 10^{- 1} {km}^{- 2}$ ，代入公式可得年龄为 $4.35 \pm 0.10 Ga$ 。2001 年更新系数后，大直径区间（ $D > 10 km$ ）的频数计算更精确，解决了早期模型在高龄区域的偏差问题。

1.2.5 软件工具与应用

Gregory Michael 开发的 Craterstats 软件（ArcGIS 插件）集成了 Neukum 模型，可自动统计撞击坑频数、拟合年龄，并绘制累积分布曲线。该工具通过标准化流程，将遥感影像中的撞击坑数据转化为地质年龄，成为月球及行星定年的重要手段。

1.3 Hartmann 撞击坑大小 - 频数累积分布的一般关系

1.3.1 基础概念与数学定义

微分分布 $n (D, t)$ ：单位面积上直径在 $D \sim D + d D$ 区间内的撞击坑数量，数学上是累积分布的导数，即 $n (D, t) = \frac{\partial N (D, t)}{\partial D}$ ，反映不同直径坑的频率密度。
累积分布 $N (D, t)$ ：单位面积上直径大于 D 的所有撞击坑总数，由微分分布积分得到： $N (D, t) = \int_{D}^{\infty} n (D^{'}, t) d D^{'}$ 。
微分撞击率 $φ (D, t)$ ：单位时间、单位面积上形成的直径 $D \sim D + d D$ 的撞击坑数量，描述撞击事件的瞬时频率。
累积撞击率 $ϕ (D, t)$ ：单位时间、单位面积上形成的直径大于 D 的撞击坑总数，是微分撞击率的积分： $ϕ (D, t) = \int_{D}^{\infty} φ (D^{'}, t) d D^{'}$ 。

1.3.2 增量频数分布模式

Hartmann（1966）提出按直径区间 $(D, p D)$ （如 $p = 2$ 或 $\sqrt{2}$ ）统计撞击坑，假设微分分布满足指数关系 $n (D, t) = A \cdot D^{α}$ ，则区间内的增量频数为：

N_{increm} = A \int_{D}^{p D} D^{' α} d D^{'} = \frac{A}{1 + α} (p^{α + 1} - 1) D^{α + 1}

由于累积分布 $N = \int_{D}^{\infty} n (D^{'}, t) d D^{'} = - \frac{A}{1 + α} D^{α + 1}$ ，可得 $N_{increm} = (1 - p^{α + 1}) N$ 。例如，当 $p = \sqrt{2}$ 时，增量频数与累积频数通过指数 $α$ 关联，适用于分析特定直径范围内的撞击坑分布特征。

1.3.3 相对分布函数 R 及其意义

定义相对分布函数R，用于检测撞击坑大小分布的小尺度扰动。

R = \frac{n (D, t)}{D^{- 3}}

若累积分布满足 $N \propto D^{- 2}$ ，则微分分布 $n \propto D^{- 3}$ ，此时 R 为常数，表明分布均匀；若累积分布满足 $N \propto D^{- 3}$ ，则 $n \propto D^{- 4}$ ， $R \propto D^{- 1}$ ，反映大直径坑的比例下降。该函数对指数变化敏感，可识别撞击过程中的异常事件（如灾变撞击导致的坑大小偏移）。

1.3.4 分段函数模型（Hartmann, 1999）

根据直径范围，将撞击坑分为三段，分别给出微分频数与累积频数的表达式：

小直径（ $D < 1.41 km$ ）： $\log N_{increm} = - 2.616 - 3.82 \log D_{L}, n (D, t) = 0.0126 D^{- 4.82}$ 其中 $D_{L}$ 为区间左边界直径，指数 $- 4.82$ 表明小坑数量随直径增大急剧减少。
中直径（ $1.41 km < D < 64 km$ ）： $\log N_{increm} = - 2.920 - 1.80 \log D_{L}, n (D, t) = 0.0047 D^{- 2.19}$ 指数 $- 2.19$ 较平缓，反映中直径坑的数量衰减速度较慢。
大直径（ $D > 64 km$ ）： $\log N_{increm} = - 2.198 - 2.20 \log D_{L}, n (D, t) = 0.0261 D^{- 3.20}$ 指数介于小坑与中坑之间，体现大撞击坑的特殊形成机制（如巨型陨石撞击）。

1.3.5 与 Neukum 模型的对比

Neukum 模型通过高阶多项式拟合全直径范围，而 Hartmann 模型采用分段指数函数，更突出不同直径区间的差异。例如，Neukum 模型在 $D = 35 km$ 处的拟合指数为 $- 1.96$ ，而 Hartmann 中直径区间的指数为 $- 2.19$ ，反映两者对中大型坑的统计差异。这种差异源于统计区域的地质背景不同（Neukum 以澄海为基准，Hartmann 侧重月海平均时间），实际应用中需根据目标区域特征选择模型。

二、陨石撞击动力学模型

1. 陨石撞击的基本过程

1.1 接触压缩阶段

撞击初始时刻（ $t = 0$ ），陨石（通常为高速运动的固态物体，速度可达 10-20 km/s）与目标表面接触，能量以冲击波形式向目标内部和陨石自身传播。目标材料在高压下迅速压缩，形成半球形的冲击压缩区，压力可达数百吉帕（GPa），远超岩石的抗压强度。例如，直径 46.4 km 的铁陨石以 15 km/s 撞击斜长岩目标时，初始接触压力可超过 100 GPa，导致目标材料瞬间熔融或汽化。此阶段持续时间极短，约为微秒至毫秒级，主要控制参数为撞击速度、陨石密度与目标材料的弹性模量。

1.2 冲击波挖掘阶段

压缩阶段后，冲击波以超声速向目标内部扩散，形成半球形的压力波前。高压区与低压区的压力梯度驱动材料高速运动，目标物质被强烈扰动，形成临时挖掘坑。冲击波的峰值压力随距离撞击点的半径 r 衰减，符合 $P \propto 1 / r^{3}$ 的规律（理想球面波近似）。同时，粒子速度在冲击前沿达到最大值，随后因能量耗散逐渐降低。该阶段中，目标材料经历塑性变形、破碎及部分熔融，形成以撞击点为中心的放射状裂隙系统，为后续溅射物抛射提供物质基础。

1.3 溅射物分离成形阶段

随着冲击波能量的衰减，目标材料的运动从压缩主导转为剪切和拉伸主导，形成 transient crater（瞬态坑）。瞬态坑初期呈半球形，半径随时间以撞击速度的 10%-20% 扩展，深度增长逐渐减缓并最终停止。此时，坑壁材料因高压冲击产生熔融层（厚度约为坑深的 10%-20%），与未熔融的破碎岩石混合。当瞬态坑半径达到最大值后，重力作用主导，坑壁开始坍塌，形成最终的撞击坑形态（如简单坑、复杂坑或盆地）。

1.4 溅射物抛射阶段

瞬态坑形成过程中，被加速的物质以弹道轨迹抛射至目标表面，形成溅射物沉积层。抛射速度与位置相关：靠近坑中心的物质获得更高速度（可达 2-5 km/s），沿陡峭轨迹远距离抛射；边缘物质速度较低（约 0.5-1 km/s），沉积在坑缘附近，形成溅射毯（ejecta blanket）。

根据 Oberbeck（1975）的理论，抛射时间 $t_{ej} \propto (r / R)^{2.8} T_{f}$ ，其中 r 为抛射点距中心距离，R 为坑半径， $T_{f} = \sqrt{D / g}$ 为特征时间（D 为坑直径，g 为目标重力加速度）。抛射物的速度分布满足 $v_{e} = 0.28 (r / R)^{- 1.8} \sqrt{g D}$ ，导致粗碎屑（低冲击损伤）集中在近坑区域，细碎屑（高冲击熔融）分布在远区，形成典型的撞击坑分层溅射结构。

2. Equations and materials in iSALE and SALEc

撞击动力学模拟依赖于多物理场耦合的数值模型，iSALE 和 SALEc 是常用的显式动力学代码，其核心包括守恒方程、材料本构模型及状态方程（EOS），以下为关键理论框架：

2.1 守恒方程

质量守恒： Lagrangian 形式:

\frac{D ρ}{D t} + ρ \nabla \cdot v = 0 $ $ 描 述 物 质 微 元 的 密 度 $ ρ $ 随 时 间 t 的 变 化 ， 其 中 $ v $ 为 粒 子 速 度 ， 物 质 导 数 $ D / D t = \partial / \partial t + v \cdot \nabla $ 包 含 随 体 运 动 的 影 响 。 E u l e r i a n 形 式 ： $ $ \partial ρ / \partial t + \nabla \cdot (ρ v) = 0

适用于固定网格下的质量输运计算。

动量守恒（Navier-Stokes 方程）：

ρ \frac{D v}{D t} = \nabla \cdot σ^{'} + g - \nabla p

其中 $σ^{'}$ 为偏应力张量（去除静水压力后的应力）， $g$ 为重力加速度，p 为静水压力。方程描述动量变化由应力梯度、重力和压力梯度共同驱动，是流体与固体运动的统一控制方程。

能量守恒：

ρ \frac{D U}{D t} = k \nabla^{2} T + H_{shear} + H_{acoustic} + H_{t} + H_{etse}

U 为比内能，k 为热导率，T 为温度。右侧包括热传导（ $k \nabla^{2} T$ ）、剪切生热（ $H_{shear}$ ）、声能耗散（ $H_{acoustic}$ ）等，其中剪切生热项与偏应力和应变率相关，是冲击过程中能量转化为内能的主要途径。

2.2 流变模型

粘性流体模型：适用于熔融或高度破碎的材料，应力 - 应变率关系为

σ_{i j} = 2 η {\dot{ε}}_{i j}

$η$ 为动力粘度， ${\dot{ε}}_{i j}$ 为应变率张量，描述材料的粘性耗散行为。

粘弹性模型：考虑材料的弹性储能与粘性耗散，应力演化方程为

\partial σ_{i j} / \partial t = 2 G {\dot{ε}}_{i j} - 2 G f (σ)

其中 G 为剪切模量， $f (σ)$ 为松弛函数（如 Maxwell 模型中 $f (σ) = 1 / (2 η)$ ），适用于冲击初期的弹性波传播阶段。

后面部分有点难了，老师也没细讲

2.3 强度模型与热软化效应

VNMS 模型（von Neumann-Mises 屈服准则）：假设材料为理想塑性体，屈服强度 $Y = Y_{0}$ 为常数，适用于高压下的金属或岩石塑性变形模拟。

ROCK 模型：考虑损伤演化的强度模型，屈服强度 $Y = Y_{d} D + Y_{i} (1 - D)$ ，其中 D 为损伤变量（0 表示完整材料，1 表示完全损伤）， $Y_{d}$ 和 $Y_{i}$ 分别为损伤后和初始屈服强度。损伤通过剪切失效（ $\sqrt{J_{2}} \geq Y_{shear}$ ）和拉伸失效（ $σ_{max}^{'} - p \geq Y_{ten}$ ）判据驱动， $J_{2}$ 为偏应力第二不变量， $Y_{shear}$ 、 $Y_{ten}$ 为剪切 / 拉伸屈服强度。

热软化模型：高温下材料强度下降，表达式为 $Y = Y_{cell} \tanh (ξ (\frac{T_{m}}{T} - 1))$ ， $T_{m}$ 为 Simon 模型定义的熔点 $T_{m} = T_{m 0} (p / a + 1)^{1 / c}$ ，随压力 p 升高而增加，描述冲击熔融对材料强度的弱化效应。

2.4 损伤模型（IVANOV 模型）

损伤变量 D 的演化方程为：

\frac{\partial D}{\partial t} = \sum_{m} {cmc}_{m} (\frac{α \sqrt{I_{2}} \cdot 1 {D_{model} = ivanov}}{max {ε_{a}, ε_{b} (p - p_{0})}} + 0 \cdot 1 {D_{model} = none})

其中 ${cmc}_{m}$ 为材料组分比例， $α = \sqrt{3 / 2}$ 为无量纲系数， $I_{2} = \frac{1}{2} {\dot{ε}}_{i j}^{2}$ 为应变率不变量， $ε_{a}$ 、 $ε_{b}$ 为损伤阈值参数， $p_{0}$ 为静水压力阈值。该模型通过应变率和压力联合控制损伤累积，适用于岩石类脆性材料的破碎过程模拟。

2.5 状态方程（EOS）

状态方程描述材料的压力 p、密度 $ρ$ 和内能 U 之间的关系，是冲击动力学的核心本构关系：

Tillotson EOS（适用于岩石、金属）：分压缩、冷膨胀、热膨胀、混合和低能量膨胀五种状态，例如压缩状态下： $p_{1} = (a + \frac{b}{E / (E_{0} η^{2}) + 1}) ρ E + A μ + B μ^{2}$ 其中 $η = ρ / ρ_{0}$ 为压缩比， $μ = η - 1$ ，E 为比内能， $E_{0}$ 为参考内能， $a, b, A, B$ 为材料常数。该方程通过经验拟合描述高压下的相变与能量耦合。
ANEOS（适用于行星内部物质）：基于亥姆霍兹自由能 $F (ρ, T) = F_{cold} (ρ) + F_{thermal} (ρ, T) + F_{electronic} (ρ, T)$ ，推导压力 $p = ρ^{2} \partial F / \partial ρ$ 、熵 $S = - \partial F / \partial T$ 和内能 $E = F + T S$ ，适用于宽范围密度和温度（如月球地壳的斜长岩和镁铁质矿物）。
Mie-Grüneisen EOS（适用于固体小压缩）：分解压力为冷压 $p_{C}$ 和热压 $p_{T}$ ： $p = p_{C} (ρ) + Γ (ρ) (E - E_{C} (ρ))$ ，其中 $Γ (ρ)$ 为 Grüneisen 参数，描述内能对压力的贡献，适用于冲击初期的弹性压缩阶段。