类地行星动力学
单体问题
重力势
1.行星重力势的一般形式
引力势的定义
引力势
引力加速度是引力势的梯度:
通常
真空中
球体的引力势
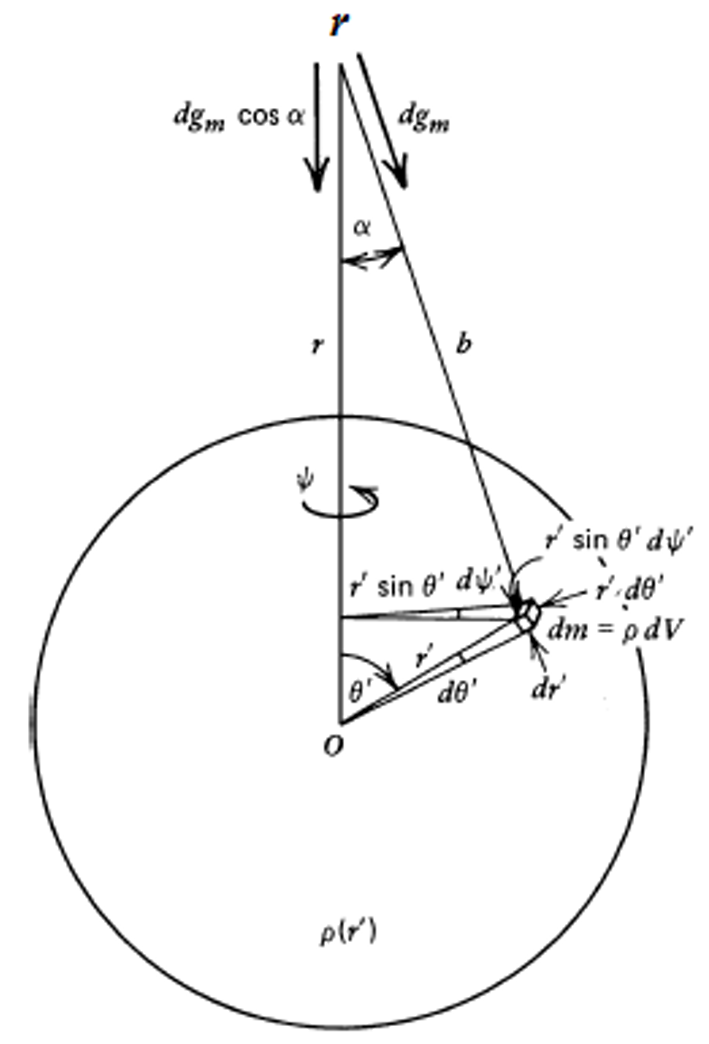
定义距离球体球心
一般轴对称质量分布:
因为
2.轴对称椭球体的重力势表达式
现在让我们来计算一个质量密度 γ 和平均半径 R 一致的椭球体外部产生的重力势能。椭球体是围绕主轴或次轴旋转椭圆而产生的固体。让旋转轴与 Z 轴重合、并让球面的外部边界满足
其中,椭圆度
现在,根据公式(1),所产生的引力势为
其中,
因此,由勒让德多项式的正交归一性知,在一阶的情况下,不为
因此重力势可以写为:
3.行星旋转的离心势一般形式
非惯性参考系——旋转参考系
行星的旋转压平
考虑一个由不可压缩流体组成的自重力天体的平衡构型,该天体围绕通过其质量中心的某个固定轴线稳定而均匀地旋转。假设天体外部边界为椭球面。假设
让我们转换到一个非惯性参照系,该参照系与身体绕 Z 轴共转,因此身体看起来是静止的。根据第 5.3 节,现在的问题类似于非旋转体的问题,只是加速度可以写成 g = gg + gc,其中 gg = -∇Φ(r,θ) 是重力加速度,gc 是离心加速度,Φ 是重力势能。离心加速度的大小为 r sinθΩ2,其方向远离旋转轴(见第 5.2 节)。(参见第 5.2 节。)这里,r 和 θ 是球面坐标,其原点是物体的几何中心,对称轴与旋转轴重合。 因此离心加速度为
转动惯量和分层模型
一旦我们从J2的测量得到转动惯量C(或者平均值I),我们可 以用2层模型来估计核幔边界
潮汐作用
1.潮汐力和潮汐隆起
潮汐力
考虑一个半径为
对于位于天体中心到质点连线(取这条连线为x轴)上的点,上式可以简化为:
由上述知,最低阶的潮汐力与受力体中心的距离成正比,与摄动天体距离的立方成反比 。天体+x部分受到的潮汐力指向+x方向,-x部分受到的潮汐力指向一 x方向。
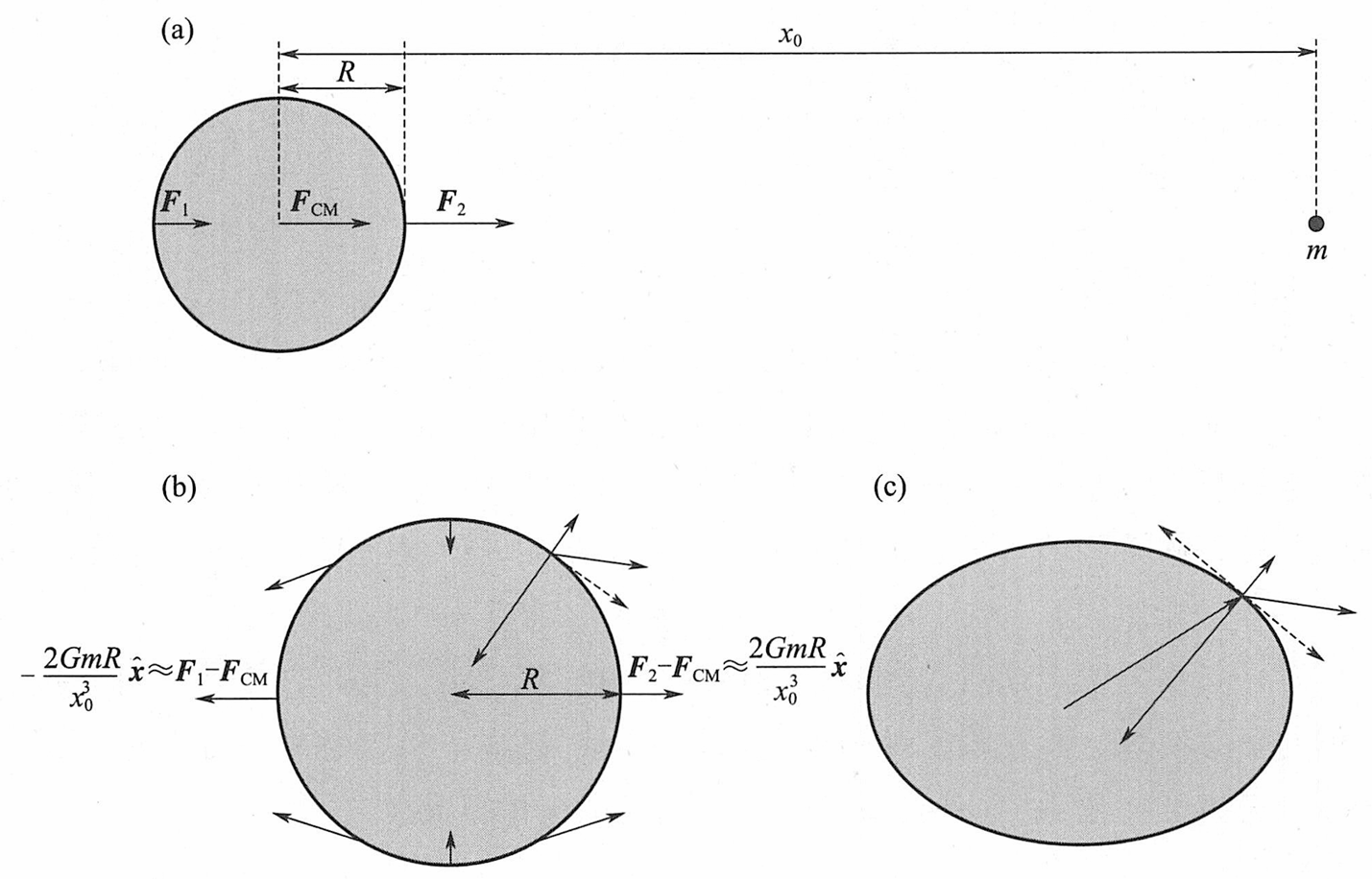
潮汐隆起
由于潮汐力的作用,x轴以外物质沿x轴方向潮汐拉伸。如果天 体是可变形的,它会在x方向上拉长。月球和地球相互之间的引力会导致潮汐隆起,沿着两个天体中心连线上升。近侧的凸起是受另一个天体引力较大的直接结果,而远侧凸起则是由于远侧所受引力小于自身中心所受引力所致。天体不同位置的离心加速度差也对潮汐隆起的大小有影响。
月球的自转和绕地球的公转同步,因此月球总是以同一面面向地球,并总在那个方向上拉长,这种现象称为潮汐锁定 。然而,地球的自转速度远远快于地月轨道周期。因此,地球指向月球的部分总在变化,并被潮汐力拉伸。与地球的固体部分相比,水更容易对这些变化的力做出反应,从而导致在海岸线看到的水位潮汐变化。由于地球自转和月球轨道运动的综合影响,月球大约每25小时经过一次地球给定的位置,因此每天几乎有两个潮汐周期,我们看到的潮汐主要是半日潮。太阳也会在地球上引发半日潮,周期为12小时,幅度略低于月球潮汐的一半。当月球、地球和太阳大致一线时,潮汐的幅度达到最大值,这种情况每个月会出现两次,即月相为新月或满月时。当月球接近近地点和地球接近近日点时(后者发生在1月初),潮汐也会更大。
潮汐影响天体结构
强烈的潮汐能显著地影响天体的物理结构。一般来说,行星对距离自身最近的卫星所施加的潮汐力,是太阳系天体感受到的最强潮汐力(除了小行星和彗星掠日或掠行星的情况以外)。在行星附近,潮汐非常强烈,它们可以撕裂一个流体(或聚集力弱的固体)天体。在这样一个区域,大卫星是不稳定的,即使是小卫星可以通过物质强度和摩擦结合在 一起,也因潮汐而无法增长。这个区域的边界称为洛希极限 。在洛希极限的内部,固体物质仍然以小天体的形式存在,我们看到的是环而不是大卫星。
2.潮汐力矩
潮汐耗散导致卫星和行星旋转速率和轨道的长期变化。虽然在没有外部力矩的情况 下,一对相互旋转天体的总角动量守恒,但角动量可以通过潮汐力矩在旋转和轨道运动之间传递。刚体旋转角动量由下式给出:
式中,
惯性张量的各分量为
3.潮汐锁定
前导半球(leading hemisphere) 和后随半球(trailing hemisphere) ,被潮汐锁定的星球始终有一面面对它所围 绕旋转的大星球,一面背对它所围绕旋转的大星球;因此也始终有一个面面对它自身轨道运动的方向,一个面背对它自身轨道运动的方向。面对它自身轨道运动方向的称为前导半球,背对自身轨道运动方向的称为后随半球
4.潮汐加热
潮汐力矩除了传递角动量,还可以传递能量。能量传输率是角动量传 输率的n倍。从式(2-19)和式(2-23)的导数与a的比值可以看出,对于一条扩大的 圆轨道,其机械能变化与轨道角动量变化之比由dE/dL=n给出。因此,由行星潮汐隆起 产生的力矩不会(直接)改变卫星轨道的偏心率。
潮汐力随时间的变化可以导致行星体内部加热。从卫星上看,当行星在天空中移动 时,具有非同步旋转的卫星潮汐隆起位置会发生变化。在偏心轨道上同步旋转的卫星经受 两类潮汐力变化。潮汐隆起的幅度随卫星与行星的距离而变化,隆起的方向也因卫星以恒 定速率(大小等于其平均轨道角速度)自转而变化,而瞬时轨道角速度则根据开普勒第二 定律而变化。由于天体不是完全刚性的,潮汐力的变化改变了卫星的形状;由于天体也不 是完全的流体,所以卫星在形状变化时会以热量的形式耗散能量。因此,在偏心轨道上或 与其轨道周期不同步旋转的天体上,潮汐变化引起的内应力会导致某些天体产生显著的潮汐加热,尤其是在木卫一上。如果没有其他力存在,由木星在木卫一上引起的潮汐变化导 致的耗散将使木卫一轨道偏心率减小。木卫一的轨道将会接近圆形,即给定角动量的最低能量状态(最小半长轴),耗散的轨道能量被转换成热能。由于木卫一 的轨道周期小于木星的自转周期,因此木卫一在木星上引起的潮汐隆起将木星的一些自转 动能转移到木卫一的轨道上,导致木卫一向外螺旋远离木星。如上所述, 这些力矩并不直接影响木卫一轨道的偏心率。然而,木卫一和木卫二之间存在2:1的平 均运动共振锁定。木卫一将它从木星得到的一些轨道能量和角动 量传递给木卫二,并且由于木卫一的轨道周期小于木卫二的轨道周期,这种传递增加了木 卫一的偏心率(习题2.29)。这种强迫偏心保持了较高的潮汐耗散率,因此木卫一有较大 的内部加热,这种加热表现为活跃的火山作用。
二体问题
月球的轨道及其演化
1.地-月二体框架下的月球轨道(开普勒轨道)
对一个只有2个行星(卫星)的系统,它们的相对运动 轨迹只用牛顿引力和初始相对运动就可以描述。
在二体问题框架下,月球轨道满足:
角动量守恒:
分解为极坐标形式:
运动方程分解:
- 速度
- 径向分量:
- 横向分量:
- 速度
开普勒定律:
- 第一定律(椭圆轨道): 微分方程(1)有一个通解,即
其中半通径
如果考虑椭圆轨道的朝向,则
其中
如果想更好地描述椭圆轨道,可以引入更多的参量,参考轨道六根数
- 第二定律(面积定律):
因为
- 第三定律:
代入后化简得:
2. 在一个轨道周期内的潮汐耗散
2.1能量耗散率:
其中
在连续介质力学中,应力张量
其中,
2.2相位延迟模型: 在实际材料中,由于材料的粘滞性质,材料在受到应力作用后,应变响应并不是瞬时的,而是存在相位差。对于潮汐变形,天体内部的材料(如岩石、冰等)在受到周期性潮汐力作用时,其应变响应会滞后于应力作用。这种滞后现象可以用相位延迟模型来描述。该模型在潮汐耗散研究中非常重要,因为它能够定量描述天体内部材料的耗散性质。
使用复数形式来表示应力和应变的关系,可以方便地引入相位延迟。复数形式的应力-应变关系可以写成:
其中,
假设应变
根据相位延迟模型,应力
将应力和应变代入能量耗散率公式,并计算在一个周期
将潮汐参数
2.3潮汐耗散系数: 潮汐耗散系数
3.月球几何天平动和物理天平动(libration)
3.1经度天平动:
3.3物理天平动:
其中
3.4章动方程:
4. 月球的长期轨道—长期扰动理论(secular perturbation)
当研究长时间尺度(secular)两个行星(卫星)之间的 相对运动时,两个行星间的变形能带来动能耗散,改变角动量;而且来自别的星体产生的小量的引力扰动可以产生巨大的改变。相应的控制方程的一般形式要修改为:
其中
拉格朗日行星方程:
其中
轨道参数演化:
- 半长轴变化:
- 偏心率演化:
- 半长轴变化:
共振效应: 当满足条件:
会导致轨道参数的剧烈变化(如evection共振)
长期演化方程: