在详细研究地球表面板块的运动(必然涉及到一些球面几何)之前,我们就先考虑一个平坦的行星来理解板块之间的相对运动。
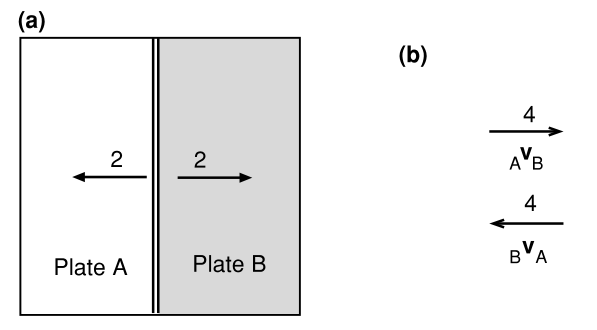
图1.1(a)构造性边界(大洋中脊)。双线是脊轴的符号,箭头和数字表示板块远离脊轴的扩张方向和相对运动方向。在这个例子中,洋脊的半扩张率(半率)为2 ;也就是说,板块A和B以4 的相对速度分离,每一个板块都在2 时生长。(b)在(a)中显示的洋脊的相对速度和。
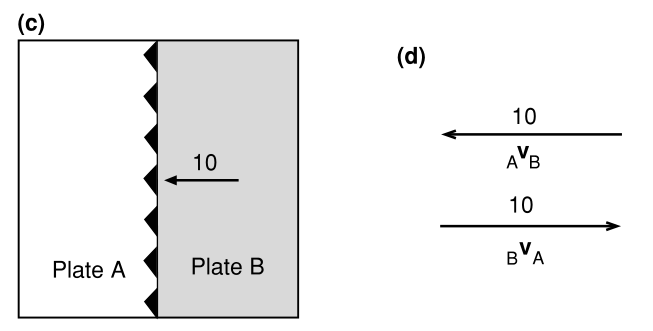
图1.1 (c)破坏性边界(俯冲带)。锯齿线表示俯冲带,锯齿位于上冲板块一侧,指向远离下沉或俯冲板块的方向。箭头和数字表示两个板块之间的相对运动方向和速度。在这个例子中,板块B以10 被俯冲。(d)在(c)中显示的俯冲带的相对速度和。
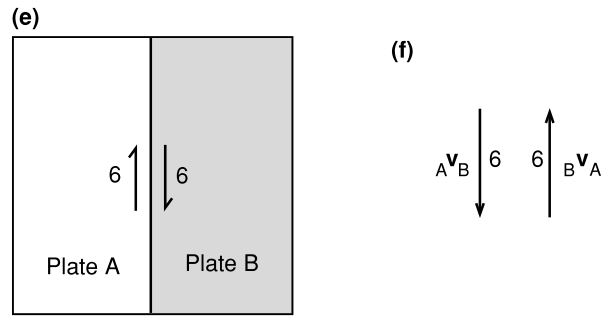
图1.1(e)守恒型边界(转换断层)。单线表示转换断层。半箭头和数字表示板块之间相对运动的方向和速度:在本例中,为6 。(f)在(e)中显示的转换断层的相对速度AVB和BVA。
图1.1显示了三种类型的板块边界以及通常在地图上描述它们的方式。为了描述两个板块 和 之间的相对运动,我们必须用一个向量来表示它们的相对运动速率(相对速度)。 板块相对于 板块的速度写为 (即,如果你是 板块上的观察者,那么 就是你看到 板块的移动速度)。反之, 板块相对于 板块的速度为 ,且
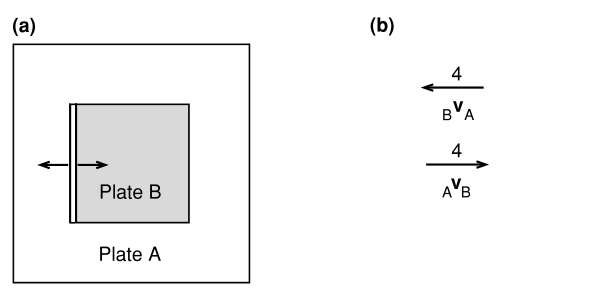
图1.2 (a)一个平坦行星上的双板块模型。板块B加了阴影。B板块的西部边界是一条脊,海底从这里以2 的半速率扩张。(b) (a)中板块的相对速度向量AVB和BVA。
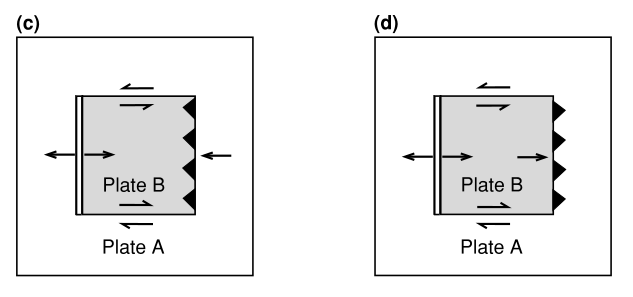
图1.2 (c) (a)中显示的模型的一个解:B板块南北边界为转换断层,东部边界为B板块上覆A板块的俯冲带。(d) (a)中显示模型的另一个解:B板块南北边界为转换断层,东部边界为A板块上覆B板块的俯冲带。
为了使我们的模型更真实,我们建立一个双板块系统(图1.2(a)),并尝试确定更复杂的运动。 板块的西部边界是一个以 2 的半速率扩张的脊。这一信息使我们能够绘制 和 (图2.5(b))。因为我们知道板块 的形状,所以我们可以看出其南北边界一定是转换断层。北部边界是左旋的(sinistral),或称左手的;当你穿过断层时,岩石向左偏移。东部边界模糊不清: 表示 板块沿此边界以 4 接近 板块,表示俯冲带在此处运作;但是没有迹象表明哪个板块正在被俯冲。图2.5(c)和(d)给出了两种可能的解。图2.5(c)显示 板块以4 速率俯冲到 板块之下。这意味着 板块以 2 的速率增宽,这个速率即在脊轴上形成新板块的速率。图2.5(d)显示 板块以 4 的速率俯冲到 A\mathrm{A} 板块之下,其速率快于在其西部边界形成新板块的速率( 2 );所以最终 B\mathrm{B} 板块将不再存在于行星表面。
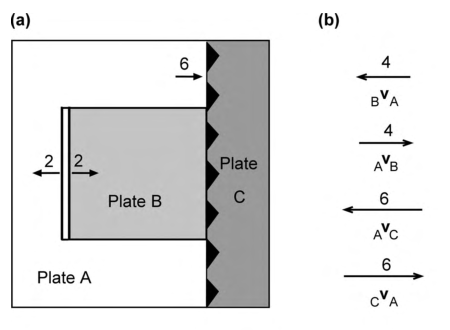
图2.6 (a)平坦行星上的三板块模型。板块A没有加阴影。板块B西部边界是一个脊,以2 的半速率扩张。板块A、C之间的边界为俯冲带,板块C以6 的速率上覆A板块。(b) (a)中所示的板块的相对速度向量。
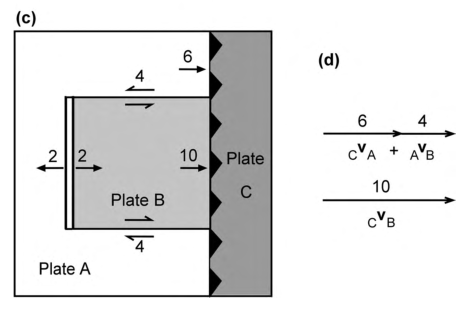
图2.6 (c) (a)中模型的解:B板块南北边界为转换断层,东部边界为俯冲带,板块C以10cm yr^(-1) 的速率上覆板块B。(d) 矢量相加来确定板块B相对于板块C的速度,CVB。
如果我们在模型中加入第三个板块,运动仍然会变得更加复杂(图2.6(a))。在本例中,板块 和 正以 2 的半速率从脊向外扩张,如图2.5(a)所示。板块 和 的东部边界为俯冲带,板块 以 6 的速率俯冲到板块 之下。板块 的存在并没有改变板块 南北边界的相对运动;这些边界是转换断层,如图2.5所示。为了确定板块 和 交界处的相对运动速率,我们必须使用向量加法:
这在图2.6(d)中得到了说明:板块 以 10 的速率俯冲到板块 之下。这意味着板块 的净破坏速率为 10-2=8 ;最终,板块 将完全俯冲,一个简单的双板块俯冲模型将开始运作。然而,如果板块 上覆了板块 ,它将以 2 的速率增宽。
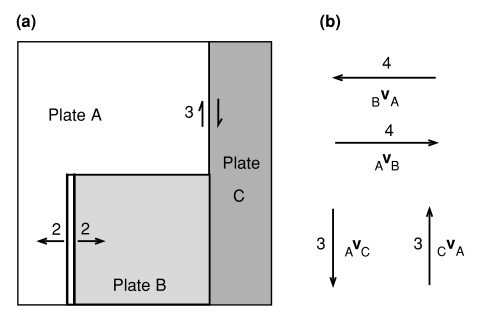
图2.7 (a)平坦行星上的三板块模型。板块A没有加阴影。板块B西部边界是一个脊,以2 的半速率扩张。板块A、C之间的边界为转换断层,相对运动速率为3 。(b) (a)中所示的板块的相对速度向量。
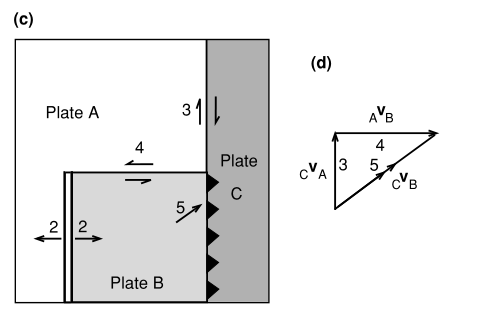
图2.7 (c) (a)中模型的稳定解:板块B的北边界为转换断层,滑动速率为4 ;板块B和C之间的边界为俯冲带,以5 的速率斜向俯冲。(d) 矢量相加来确定板块B相对于板块C的速度,CVB。
到目前为止,所有例子中的相对运动都是朝东西方向的,使得例子很简单。(向量加法不是必须的,用常识判断同样有效。)现在我们把南北方向的运动也考虑进来。图2.7(a)显示了 、 和 三个板块的模型:板块 的西部边界是一个以 2 的半速率扩张的脊,板块 的北部边界是一个转换断层(正如在其他例子中一样)而且板块 、 之间的边界为相对运动速率为 3 的转换断层。板块 和 之间的边界处的运动是未知的,必须用公式(2.2)来确定。对于这个例子,有必要画一个向量三角形来确定 (图2.7(d))。此问题的一个解如图2.7(c)所示:板块 以 5 的速率斜向俯冲到板块 下方。另一个可能的解是板块 以 5 的速率俯冲到板块 下方。在这种情况下,板块 和 之间的边界将不会与板块 和 之间的边界保持共线关系,而是稳定地向东移动。(这是一个**三重联接(triple junction)**不稳定的例子;参见2.6节)。
这些例子应该能让我们了解一下当板块相对运动时会发生什么、以及不同情况下产生的板块边界的类型。本章末尾的一些问题涉及到平坦地球,就像我们在这些例子中假设的那样。然而,真实的地球是球形的,所以我们需要使用一些球面几何学。








